1. Để tìm các đa thức P(x) thỏa mãn điều kiện P(2014) = 2046 và P(x) = P(x^2 + 1) - 33 + 32, ∀x ≥ 0, ta có thể sử dụng phương pháp đệ quy. Bước 1: Xác định bậc của đa thức P(x). Vì không có thông tin về bậc của đa thức, chúng ta sẽ giả sử nó là một hằng số n. Bước 2: Xây dựng công thức tổng quát cho đa thức P(x). Với bậc n đã xác định, ta có: P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2014 vào biểu thức và giải phương trình: P(2014) = a_n * (2014)^n + a_{n-1} * (2014)^{n-1} + ... + a_0 = 2046 Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): P(x) = P(x^2+1)-33+32 Áp dụng công thức này lặp lại cho đến khi đạt được kết quả cuối cùng. 2. Để tìm các đa thức P(x) ∈ Z[x] bậc n thỏa mãn điều kiện [P(2x)]^2 = 16P(x^2), ∀x ∈ R, ta có thể sử dụng phương pháp đệ quy tương tự như trên. Bước 1: Xác định bậc của đa thức P(x). Giả sử bậc của P(x) là n. Bước 2: Xây dựng công thức tổng quát cho P(x): P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2x vào biểu thức và giải phương trình: [P(2x)]^2 = (a_n * (2x)^n + a_{n-1} * (2x)^{n-1} + ... + a_0)^2 = 16P(x^2) Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): [P(4x)]^2 = (a_n * (4x)^n + a_{n-1} * (4x)^{n-1} + ... + a_0)^2 = 16P(x^2) Lặp lại quá trình này cho đến khi đạt được kết quả cuối cùng.

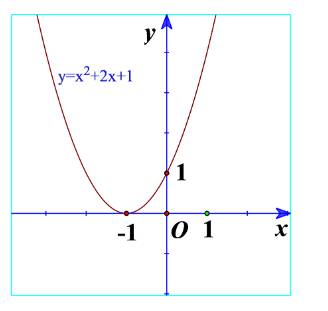
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)

Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)

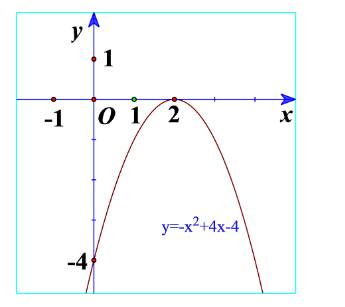
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)

Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)

c) Nếu \(\Delta  = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)

Tại sao lại không? Phương trình này lúc nào chả có nghiệm. Bạn ra đề rõ ràng nhé!!!

Đề là thế đó bạn , đa thức trên ko phân tích đc thành nhân tử và bạn hãy cm điều đó đi,  gợi ý dùng đ/l bê du ấy, nếu bạn chắc chắn đề sai thì hãy thử phân tích thành nhân tử đi!!!!

Bạn xem lại đề

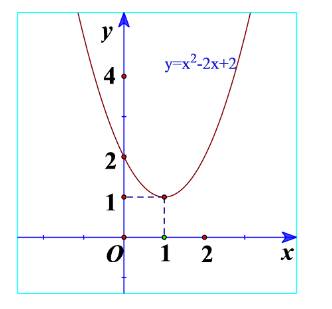
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).

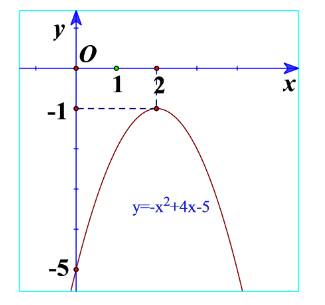
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) =  - {x^2} + 4x - 5 < 0\).

c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)

\(f\left( x \right) =  - {x^2} + 4x - 5\) có hệ số a=-1

Như thế, khi \(\Delta  < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.

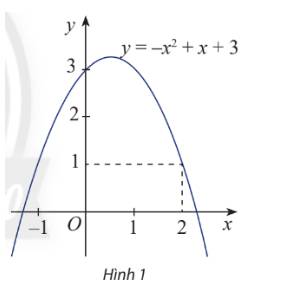
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai

b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:

\(f\left( 2 \right) =  - {2^2} + 2 + 3 = 1 > 0\)

Suy ra \(f\left( 2 \right)\) dương.