
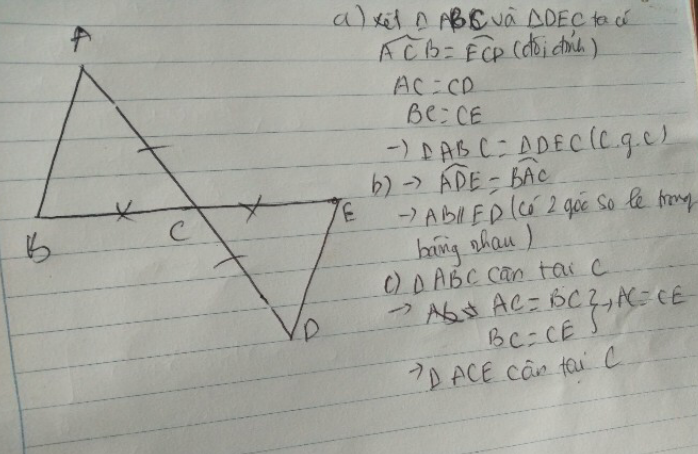
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

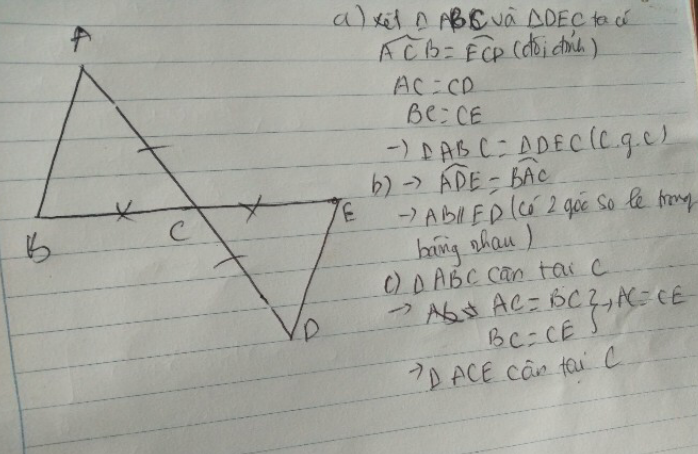

a, Vì tam giác ABC cân tại A nên AB=AC;B=C
Xét tam giác AEB và tam giác ADC có:
Góc A chung
AB=AC(cmt)
AD=AE(gt)
=> Tam giác ADC=tam giác AEB
=>BE=CD và góc ABE= góc ACD
b, Ta có
A+B+C=180(tổng 3 góc của tam giác)
B+C=180-A (1)
Và A+D+E=180
D+E=180-A (2)
Từ (1) và (2)=>B+C=D+E
Mà B=C và D=E
=>C=E
Mà 2 góc ở vị trí đồng vị
=>DE//BC
c, Ta có
B=C (cmt)
góc ABE= góc ACD(cm ở câu a)
Mà B-ABE=EBC
và C-ACD=DCB
=> góc EBC = góc DCB
=> tam giác KBC cân tại K

a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
b) Ta có: ΔABD=ΔACD(cmt)
nên BD=CD(hai cạnh tương ứng)
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
c) Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
Xét ΔADC có
H là trung điểm của CD(gt)
HE//AD(cùng vuông góc với BC)
Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(cmt)
mà DE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)
nên \(DE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay DE=EC
Xét ΔDEC có ED=EC(cmt)
nên ΔDEC cân tại E(Định nghĩa tam giác cân)

(hình bạn tự vẽ nhé)
a) ta có:tam giác ABC=tam giác DCB (g.c.g)(1)
tam giác BED=tam giác DCB(g.c.g) (2)
Từ (1),(2)→tam giác ABC=tam giác BED (dfcm)
b) Tương tự câu a, ta chứng minh được ΔABC=ΔCDF
→AC = CF suy ra F là trung điểm của AF
c)Tương tự câu b, ta chứng minh được AB=BE,ED=DF
suy ra BF,CE là đường trung tuyến của ΔAEF
suy ra G là trọng tâm

Xét tam giác ABE và tam giác ADC:
AE=AC(theo gt tam giác ABC cân )
góc A chung
AE=AD(theo gt)
=> Tam giác ABE=tam giác ADC(c.g.c)
nên BE=CD(dpcm)
Vì tam giác ABE=tam giác ACD nên góc ABE=góc ACD( 2 góc tương ứng)
Xét Tam giác DIB và tam giác EIC
góc DKB=góc EKC(đối đỉnh)
AB=AC(tam giác ABC cân) mà AD=AE (gt) =>DB=EC
góc DBI= góc ECI
=>tam giác DIB=tam giác EIC(g.c.g)
=>IB=IC(2 cạnh tương ứng)
=>tam giác IBC là tam giác cân
ĐÚNG NHA
a) Xét \(\Delta ADC\) và \(\Delta AEB\) có:
góc A chung; AB=AC (\(\Delta ABC\) cân tại A) ; AD=AE (gt)
-> \(\Delta ADC\)=\(\Delta AEB\) (c.g.c)
b) Vì \(\Delta ADC\)=\(\Delta AEB\) nên góc ABE = góc ACD (góc tương ứng) (1)
Vì \(\Delta ABC\) cân tại A nên góc ABC = góc ACB (hai góc ở đáy) (2)
Trừ vế theo vế của (2) và (1) ta được: góc ABC - góc ABE = góc ACB - góc ACD
Hay góc IBC = góc ICB
-> Tam gics IBC cân tại I

a) Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
BC2= AB2 +AC2
=> BC =\(\sqrt{AB^2+AC^2}\)=\(\sqrt{5^2+12^2}\)=13 (cm)
Trả lời (Tự vẽ hình)
a) \(\Delta ABC\)vuông tại A
=> Áp dụng định lý Pi-ta-go
Ta có: \(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\)
\(\Rightarrow BC=13\left(cm\right)\)
Vậy BC=13 (cm)
b) Xét \(\Delta ABC\&\Delta ADC\)có:
AC chung (1)
\(\widehat{BAC}\)\(=\widehat{CDA}\)\(\left(=90^o\right)\left(2\right)\)
\(AB=AD\left(gt\right)\left(3\right)\)
(1)(2)(3)\(\Rightarrow\Delta ABC=\Delta ADC\)
Vậy \(\Delta ABC=\Delta ADC\left(đpcm\right)\)
c) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\hept{\begin{cases}c_1=c_2\left(cmt\right)\\BC=AE\left(gt\right)\\CEA=c_1\end{cases}\Rightarrow\Delta AEC}\)cân
Vậy \(\Delta AEC\)cân (đpcm)
\(\)

a:\(\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=90^0+\widehat{BAC}\)
Do đó: \(\widehat{DAC}=\widehat{BAE}\)
Xét ΔDACvà ΔBAE có
AD=AB
\(\widehat{DAC}=\widehat{BAE}\)
AC=AE
Do đó: ΔDAC=ΔBAE
=>DC=BE
b: ΔDAC=ΔBAE
=>\(\widehat{ADC}=\widehat{ABE};\widehat{ACD}=\widehat{AEB}\)
\(\widehat{CEB}+\widehat{ECD}\)
\(=\widehat{CEB}+\widehat{ECA}+\widehat{DCA}\)
\(=\widehat{ECA}+\widehat{AEB}+\widehat{CEB}\)
\(=\widehat{ECA}+\widehat{AEC}=90^0\)
=>BE\(\perp\)CD

b) Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AD=AE(gt)
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC(cmt)
\(\widehat{DBC}=\widehat{ECB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔDBC=ΔECB(c-g-c)
Suy ra: \(\widehat{BDC}=\widehat{CEB}\)(hai góc tương ứng)
hay \(\widehat{KDB}=\widehat{KEC}\)
Ta có: ΔABE=ΔACD(cmt)
nên \(\widehat{ABE}=\widehat{ACD}\)(hai góc tương ứng)
hay \(\widehat{DBK}=\widehat{ECK}\)
Xét ΔDBK và ΔECK có
\(\widehat{KDB}=\widehat{KEC}\)(cmt)
DB=EC(cmt)
\(\widehat{DBK}=\widehat{ECK}\)(cmt)
Do đó: ΔKBD=ΔKCE(g-c-g)
a) Sửa đề: BE=DC
Xét ΔABE và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}\) chung
AE=AD(gt)
Do đó: ΔABE=ΔACD(c-g-c)
Suy ra: BE=CD(hai cạnh tương ứng)