Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(K đăng hình đc nên hình tự vẽ)
Kẻ \(AH\perp BC\left(H\in BC\right)\)
• Xét \(\Delta HAC\) vuông tại \(H\) có
\(\sin C=\dfrac{AH}{AC}\Rightarrow AH=\sin50^o.35\approx26,81\left(cm\right)\)
\(\cos C=\dfrac{HC}{AC}\Rightarrow HC=\cos50^o.35\approx22,5\left(cm\right)\)
• Xét \(\Delta HAB\) vuông tại \(H\) có
\(\tan B=\dfrac{AH}{BH}\Rightarrow BH\approx\dfrac{26,81}{\tan60^o}\approx15,48\left(cm\right)\)
\(\cos B=\dfrac{AH}{AB}\Rightarrow AB\approx\dfrac{26,81}{\cos60^o}\approx53,62\left(cm\right)\)
*Khi đó chu vi \(\Delta ABC\) bằng \(AB+BC+AC\)
\(\approx53,62+\left(22,5+15,48\right)+35\)
\(\approx192,48\left(cm\right)\)
*Khi đó \(S_{\Delta ABC}=\dfrac{AH.BC}{2}\approx\dfrac{26,81.\left(22,5+15,48\right)}{2}\approx509,12\left(cm^2\right)\)
#F.C

a: Xét ΔAHB vuông tại H có sin B=AH/AB
nên AB=5,96(cm)
=>BH=2,52(cm)
Xét ΔAHC vuông tại H có sin C=AH/AC
nên AC=7,05(cm)
=>HC=4,53(cm)
BC=2,52+4,53=7,05(cm)
C=7,05+7,05+5,96=20,06(cm)
b: góc A=180-58-40=82 độ
Xét ΔBHA vuông tại H có tan A=BH/HA
nên HA=0,56(cm)
Xét ΔBHC vuông tại H có tan C=BH/HC
nên HC=4,77(cm)
=>AC=5,33(cm)
\(S_{ABC}=\dfrac{5.33\cdot4}{2}=10.66\left(cm^2\right)\)

a) Áp dụng HTL ta có:\(MH.HP=MH^2\Rightarrow x=\sqrt{2.8}=4\)
\(BC=MH+HP=10\)
Áp dụng HTL ta có: \(HP.NP=MP^2\Rightarrow y=\sqrt{8.10}=4\sqrt{5}\)
b) Áp dụng HTL ta có: \(EQ.QF=DQ^2\Rightarrow x=\dfrac{4^2}{1}=16\)
\(EF=EQ+QF=17\)
Áp dụng HTL ta có: \(QP.EF=y^2\Rightarrow y=\sqrt{17.1}=\sqrt{17}\)

a: góc ACM=1/2*sđ cung AM=90 độ
góc BAD+góc ABD=90 độ
góc MAC+góc AMC=90 độ
mà góc ABD=góc AMC
nên góc BAD=góc MAC
b: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp

Kẻ đường cao BH ⊥ AC tại H
Tam giác ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\widehat{A}=180^o-20^o-30^o=130^o\)
Xét tam giác BHC vuông tại H có :
+) sin C = \(\frac{BH}{BC}\) <=> BH = \(BC.\sin30^o\) = 30 mm
+) cos C = \(\frac{CH}{BC}\) <=> CH = \(BC.\cos30^o\) = \(30\sqrt{3}\) mm
Vì \(\widehat{BAC}+\widehat{BAH}=180^o\)
mà \(\widehat{BAC}=130^o\)
=> \(\widehat{BAH}=50^o\)
Xét tam giác ABH vuông tại H có :
tan A = \(\frac{BH}{AH}\) <=> AH = \(30\div\tan50^o\) \(\approx\) 25 mm
=> AC = HC - AH = \(30\sqrt{3}\) - 25 \(\approx\) 27 mm
=> \(S_{ABC}=\) \(\frac{BH.AC}{2}\) = 405 \(mm^2\)

Có \(\widehat{B}=180^0-105^0-30^0=45^0\)
Kẻ AH vuông góc với BC
\(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A
\(\Rightarrow AH=BH\)
Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)
\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm2)
Vậy...

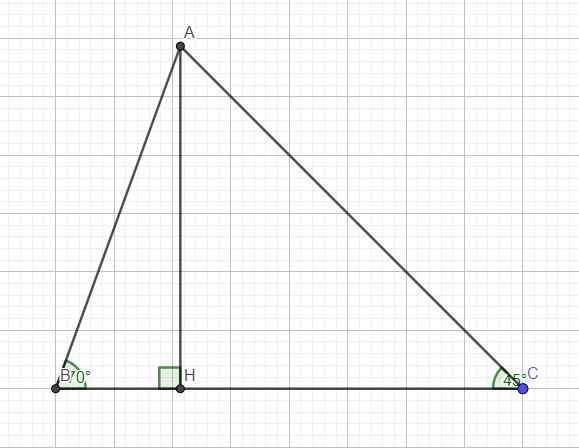
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)