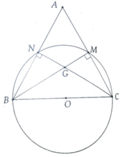
a, Ta có:  B N C ^ = 90 0 => N ∈ (O; B C 2 )

B M C ^ = 90 0 => M ∈ (O; B C 2 )

=> B, C, M, N cùng thuộc đường tròn tâm (O; B C 2 )

b, ∆ABC đều có G là trực tâm đồng thời là trọng tâm

∆AOB vuông tại O có R = ON =  a 2

Ta có OA =  a 2 - a 2 4 = a 3 2 > R

=> A nằm ngoài (O)

Ta có OG = 1 3 OA =  a 3 6 < R

=> G nằm ngoài (O)

a: góc BMC+góc BNC=90+90=180 độ

=>BMCN nội tiếp

b: Xét ΔAFM và ΔAMK có

góc AMF=góc AKM

góc FAM chung

=>ΔAFM đồng dạng với ΔAMK

=>AF/AM=AM/AK

=>AM^2=AF*AK

a: Xét tứ giác BNMC có góc BNC=góc BMC=90 độ

nên BNMC là tứ giác nội tiếp

=>B,N,M,C cùng thuộc (O)

b: Xét (O) có

BC là đường kính

MNlà dây

Do đó: BC>MN

c: Vì ΔABC đều có G là giao của hai đường cao

nên G là tâm đường tròn ngoại tiếp ΔABC và cũng là trọng tâm

=>GA=GC và AG=2/3AO

=>GC>GO

=>G nằm trong (O)

a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)

=>MBOC là tứ giác nội tiếp

=>M,B,O,C cùng thuộc một đường tròn

b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)

Xét (O) có

MB,MC là các tiếp tuyến

Do đó: MB=MC

=>M nằm trên đường trung trực của BC(1)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra MO là đường trung trực của BC

=>MO\(\perp\)BC tại H và H là trung điểm của BC

Xét ΔOBM vuông tại B có BH là đường cao

nên \(OH\cdot HM=HB^2\)

=>\(OH\cdot HM=HB\cdot HC\)

a, Ta có AC ; AB lần lượt là tiếp tuyến (O) với C;B là tiếp điểm 

=> ^ACO = ^ABO = 90⁰

Xét tứ giác ABOC có 

^ACO + ^ABO = 180⁰ 

mà 2 góc này đối 

Vậy tứ giác ABOC là tứ giác nt 1 đường tròn

hay các điểm A;B;O;C cùng thuộc 1 đường tròn 

b, Ta có AB = AC ( tc tiếp tuyến cắt nhau ) 

OC = OB = R 

Vậy OA là đường trung trực đoạn BC 

=> OA vuông BC 

Xét tam giác ACO vuông tại C, đường cao CH 

Ta có AC^2 = AH.AO ( hệ thức lượng ) 

Xét tam giác ACE và tam giác ADC 

^A _ chung 

^ACE = ^ADC ( cùng chắn cung CE ) 

Vậy tam giác ACE ~ tam giác ADC (g.g) 

\(\dfrac{AC}{AD}=\dfrac{AE}{AC}\Rightarrow AC^2=AE.AD\)

=> AH . AO = AE . AD (*)

Xét tam giác AHE và tam giác ADO ta có 

AH/AD = AE/AO ( tỉ lệ thức * ) 

^A _ chung 

Vậy tam giác AHE ~ tam giác ADO (g.g) 

=> ^AHE = ^ADO (1) 

Lại có ^ACE = ^CDE ( cùng chắn cung CE ) (2) 

Lấy (1) + (2) ta được ^BDC = ^AHE + ^ACE 

dm có ông nào giải hộ tôi điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

a: Xét tứ giác MAOB có 

\(\widehat{OAM}+\widehat{OBM}=180^0\)

Do đó: MAOB là tứ giác nội tiếp

a) Ta có

MAMA là tiếp tuyến của đường tròn (gt)

 ⇒⇒ MA⊥OAMA⊥OA => ˆMAO=90°MAO^=90° 

MBMB là tiếp tuyến của đường tròn (gt)

 ⇒⇒ MB⊥OBMB⊥OB => ˆMBO=90°MBO^=90°

Xét tứ giác MAOBMAOB có ˆMAO+ˆMBO=180°MAO^+MBO^=180° mà chúng ở vị trí đối nhau

⇒⇒ tứ giác MAOBMAOB là tứ giác nội tiếp 

⇒⇒ M,A,O,BM,A,O,B cùng thuộc 11 đường tròn

b) Ta có MA,MBMA,MB là 2 tiếp tuyến cắt nhau tại MM

⇒⇒ MA=MBMA=MB ⇒⇒ MOMO là tia phân giác ˆAMBAMB^

Xét ΔAMI∆AMI và ΔBMI∆BMI 

Có MA=MBMA=MB (cmt)

ˆAMI=ˆBMIAMI^=BMI^ (cmt) 

MIMI chung => ΔAMI=ΔBMI∆AMI=∆BMI (c.g.c)

⇒⇒ ˆAIM=ˆBIMAIM^=BIM^ 

Mà ˆAIM+ˆBIM=180°AIM^+BIM^=180° (kề bù)

⇒⇒ ˆAIM=180°2=90°AIM^=180°2=90°

⇒⇒ MO⊥ABMO⊥AB tại II

c) Ta có: ˆBDC=90°BDC^=90°(Góc nội tiếp chắn đường kính BCBC) 

⇒⇒ ΔBDC∆BDC vuông tại D⇒BD⊥CDD⇒BD⊥CD

ΔBCM⊥BΔBCM⊥B (do BMBM là tiếp tuyến của (O))

Hệ thức lượng vào ΔBCM⊥B,BD⊥CDΔBCM⊥B,BD⊥CD (chứng minh trên) ta có:

BM2=MD.MCBM2=MD.MC (1)

Xét ΔMAO∆MAO vuông tại A

AI⊥OMAI⊥OM (Vì AB⊥OMAB⊥OM) ⇒⇒ AM2=MI.MOAM2=MI.MO (2)

mà AM=BMAM=BM (tính chất hai tiếp tuyến cắt nhau) (3) 

Từ (1), (2) và (3) ⇒⇒ MD.MC=MA2=MI.MOMD.MC=MA2=MI.MO

d) Xét ΔEOM∆EOM cà ΔIOF∆IOF 

ˆEOMEOM^ chung 

ˆOIF=ˆOEM=90°OIF^=OEM^=90° (gt &cm)

⇒⇒ ΔEOM∼ΔIOF∆EOM∼∆IOF (g.g)

⇒⇒ OEOI=OMOFOEOI=OMOF (tỉ số đồng dạng)

⇒⇒ OE.OF=OM.OIOE.OF=OM.OI

Lại có ΔOAM∆OAM vuông tại AA

Mà AI⊥OMAI⊥OM (cmt)

⇒⇒ OA2=OI.OMOA2=OI.OM Mà OA=OC=ROA=OC=R

⇒⇒ OC2=OF.OEOC2=OF.OE

⇒⇒ OCOE=OFOCOCOE=OFOC

Xét ΔOCF∆OCF và ΔOCE∆OCE có 

ˆCOFCOF^ chung 

OCOE=OFOCOCOE=OFOC

⇒⇒ ΔOCF∼ΔOEC∆OCF∼∆OEC (c.g.c)(c.g.c)

⇒⇒ ˆOFC=ˆOCE=90°OFC^=OCE^=90°

⇒⇒ OC⊥CFOC⊥CF tại C

⇒⇒ FCFC là tiếp tuyến của đường tròn 

(ĐPCM)

b: Xét tứ giác ANHM có 

\(\widehat{ANH}+\widehat{AMH}=180^0\)

Do đó: ANHM là tứ giác nội tiếp

hay A,N,H,M cùng thuộc 1 đường tròn