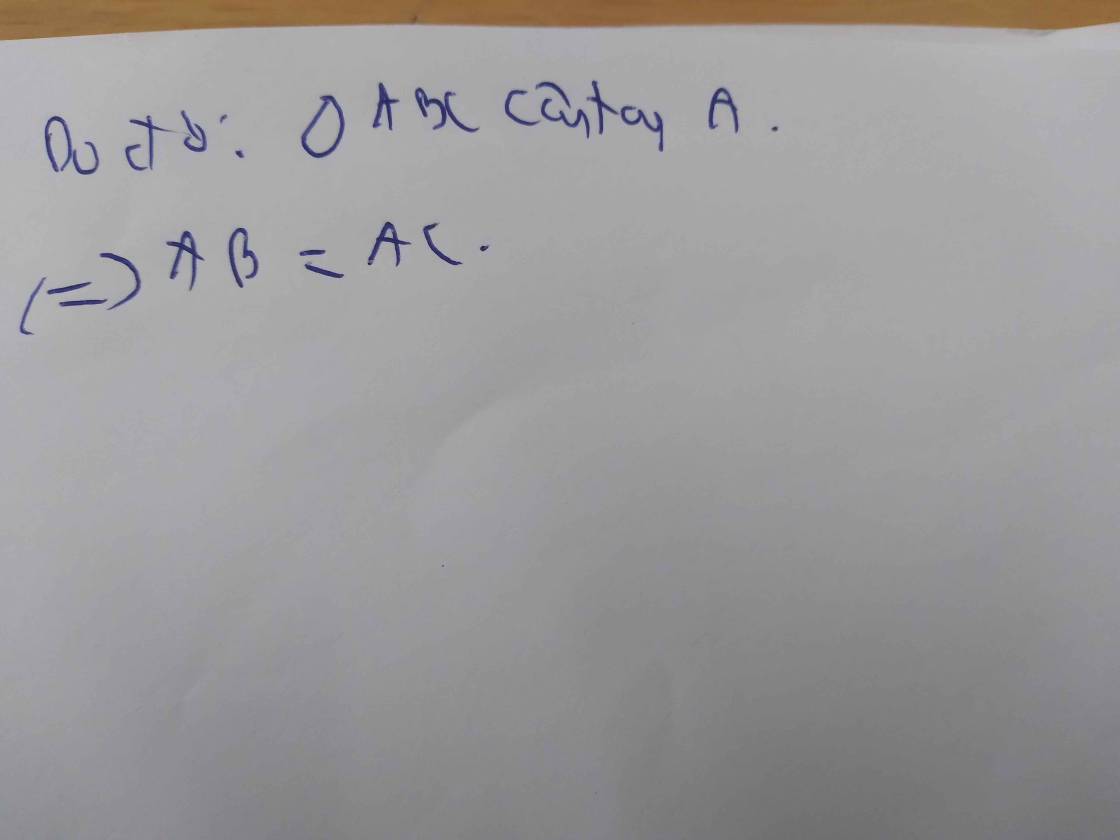Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
MN//BC
nên \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
=>\(\dfrac{AN}{NC}=1\)
=>AN=NC
b: Xét tứ giác AICK có
N là trung điểm chung của AC và KI
=>AICK là hình bình hành
c: Xét ΔABC có AI là phân giác
nên \(\dfrac{IB}{IC}=\dfrac{AB}{AC}\)
\(\dfrac{MB}{NC}=\dfrac{AB}{2}:\dfrac{AC}{2}=\dfrac{AB}{AC}\)
=>\(\dfrac{IB}{IC}=\dfrac{MB}{NC}\)
=>\(IB\cdot NC=MB\cdot IC\)

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

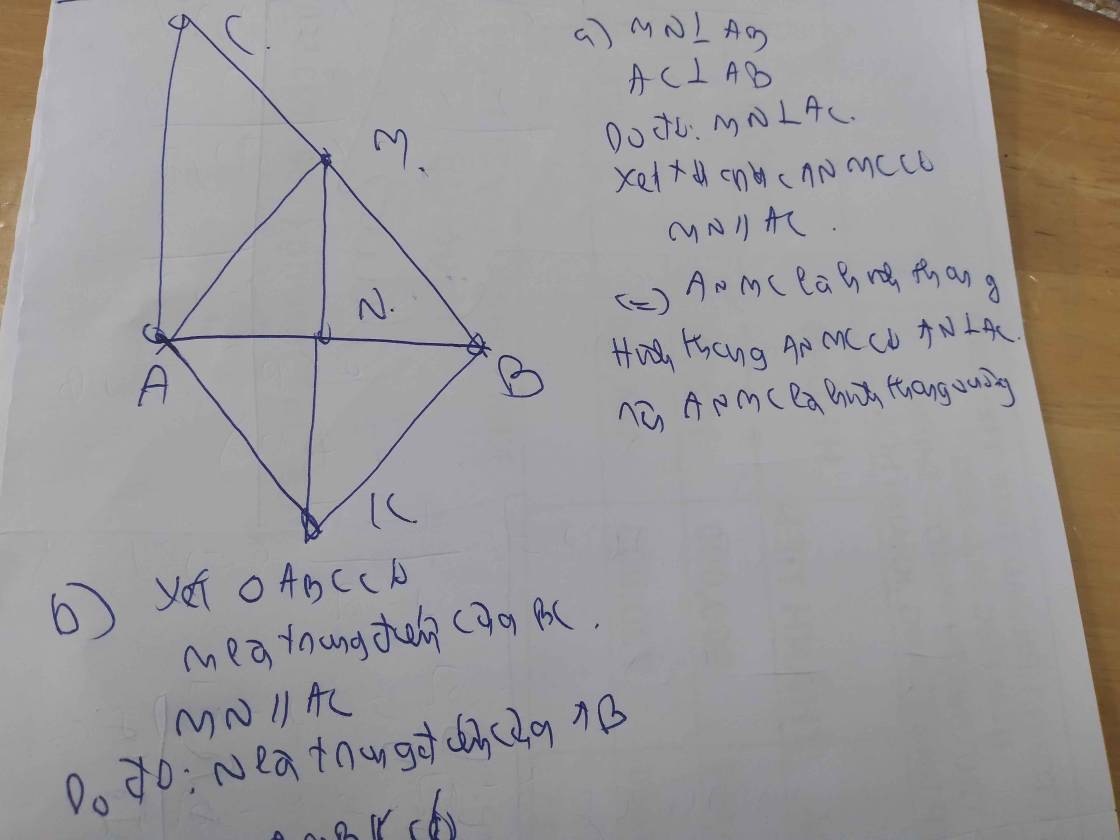
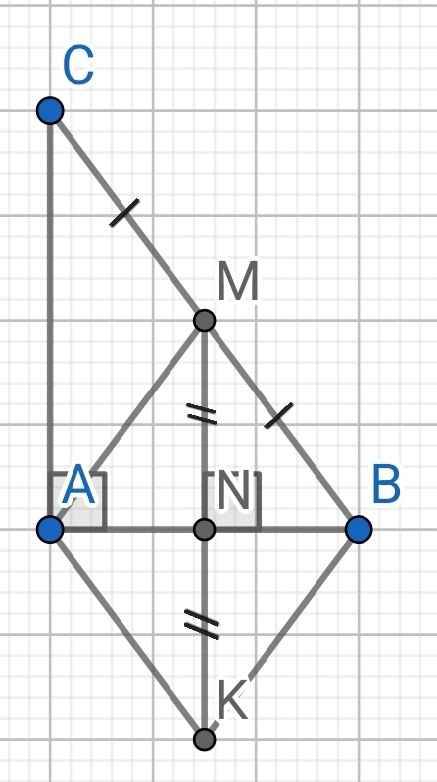 a) Do MN ⊥ AB (gt)
a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A