Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tứ giác AOBM nội tiếp thì có tâm đường tròn là trung điểm OM
cần CM tứ giác OIMB nội tiếp: dùng tổng hai góc đối cộng với nhau bằng 180o, mà đã có OBM=90o, mà I là trung điểm dây cung CD nên OI vuông góc CD luôn => OIM=90o
Vậy tứ giác OIMB nội tiếp thì tâm đường tròn cũng tại trung điểm OM luôn
b) 5 điểm A,I,O,B,M cùng thuộc 1 đtron
=> tứ giác AIOB nội tiếp => góc AIB=AOB (cùng chắn cung)
tứ giác AIOM nội tiếp => góc AIM=AOM (ccc)
mà góc AOM=1/2AOB=AIM=1/2AIB
=> BIM=1/2AIB (đpcm

a) Ta có
OA vg góc vs MA (gt) => góc MAO = 90 độ
OB vg góc vs MB (gt) => góc MBO = 90 độ
Tứ giác MAOB có góc MAO + góc MBO = 90 + 90 = 180 độ
=> MAOB nội tiếp
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC=OM^2-R^2
b: Xét (O) co
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2=MC*MD
=>MH/MD=MC/MO
=>ΔMHC đồng dạng vơi ΔMDO
=>góc MHC=góc MDO
=>góc ODC+góc OHC=180 độ
=>OHCD nội tiếp

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=180^0\)
nên MAOB là tứ giác nội tiếp(1)
Xét tứ giác OHMB có \(\widehat{OHM}+\widehat{OBM}=180^0\)
nên OHMB là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,H,A,M,B cùng thuộc đường tròn
b: Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó:ΔMAC\(\sim\)ΔMDA
Suy ra: MA/MD=MC/MA
hay \(MA^2=MD\cdot MC=MO^2-R^2\)
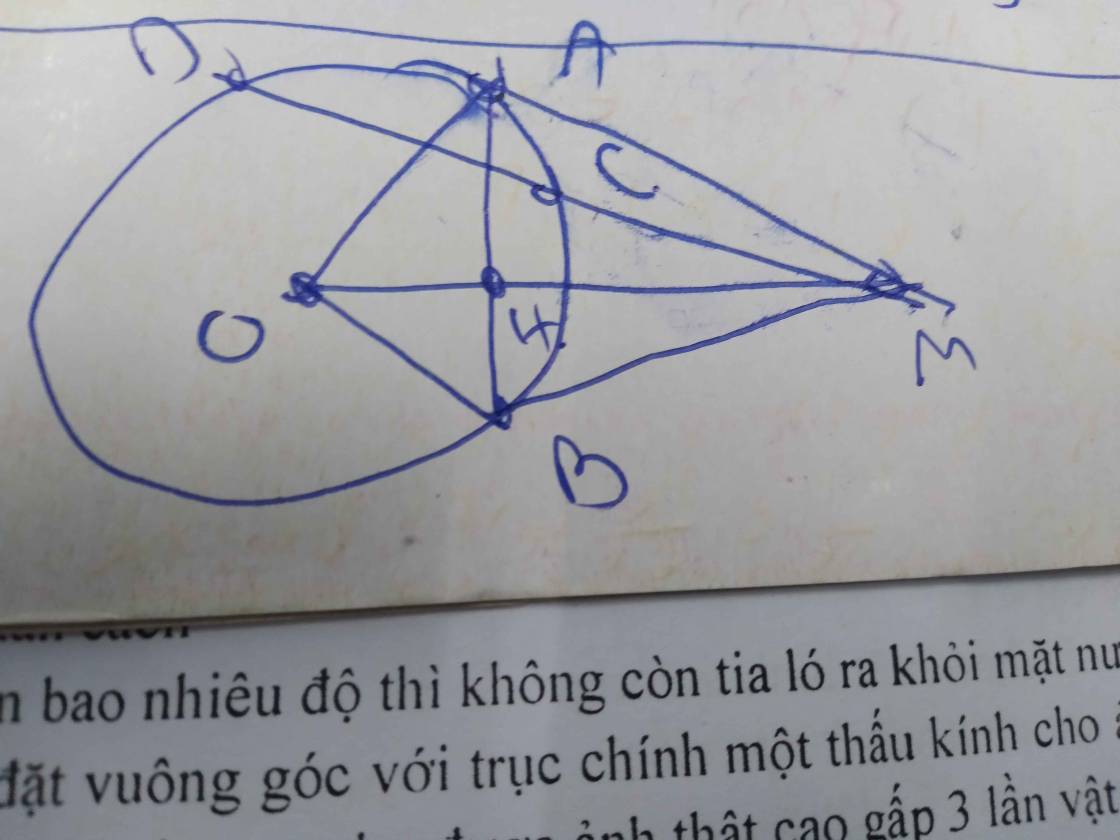

vì AM là tiếp tuyến của ( O) => OA⊥AM =>ΔOAM vuông ở A
=> điểm A thuộc đường tròn đường kính OM
vì BM là tiếp tuyến của (O) => OB⊥BM =>ΔOBM vuông ở B
=> điểm B thuộc đường tròn đường kính OM
Vì OH⊥MI=>ΔOHM vuông tại H
=> điểm H thuộc đường tròn đường kính OM
=> 4 điểm O,A,M,B,H cùng thuộc đường tròn đường kính OM