Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(MD\perp AB\) (gt)
\(AC\perp AB\) (gt)
=> MD//AC (1) \(\Rightarrow\widehat{BMD}=\widehat{C}\) (góc đồng vị)
Mà \(\widehat{B}=\widehat{C}\) (gt)
\(\Rightarrow\widehat{B}=\widehat{BMD}\) => tg BMD vuông cân tại D => MD=BD (2)
\(ME\perp AC\) (gt)
\(AB\perp AC\) (gt)
=> ME//AB (3)
C/m tương tự ta cũng có tg CME vuông cân tại E => ME=CE (4)
Từ (1) và (3) => ADME là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau)
=> MD = AE (5) và ME = AD (6)
Ta có
\(C_{ADME}=\left(MD+ME\right)x2\)
AE = AC-CE Từ (5) => MD=AC - CE Từ (4) => MD = AC - ME
\(\Rightarrow C_{ADME}=\left(AC-ME+ME\right)x2=2xAC\) không đổi

dòng này tôi viết vì có việc nhé ko phải là tl linh tinh mong thông cảm và cũng ko phải là nội dung bài làm nhé.

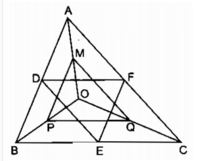
Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:
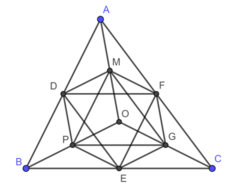
DP = QF (vì bằng 1/2 OA);
PE = MF (vì bằng 1/2 OC)
EQ = MD (vì bằng 1/2 OB)
Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.
Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.