Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
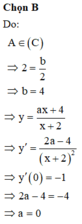
- Phương trình hoành độ giao điểm của d và (C) là
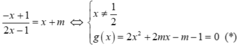
- Theo định lí Viet ta có x1+x2=-m; 
Giả sử A( x1; y1); B( x2; y2).
- Ta có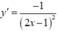 
nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là 
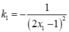và 
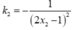.Vậy
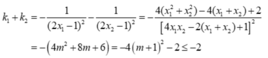
- Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng -2 khi m= -1.
Chọn A.
+ Phương trình hoành độ giao điểm của d và (C) là
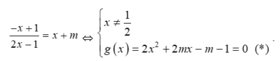
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2
Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
Hệ số góc của đường thẳng IM là:
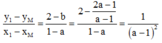
Mặt khác tiếp tuyến tại M có hệ số góc k = y ' ( a ) = - 1 ( a - 1 ) 2
Giả thiết bài toán
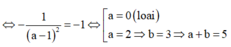
Chọn C.
Câu 1:
\(f'\left(1\right)=g'\left(1\right)=k\)
\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)
\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)
Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)
\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)
\(\Rightarrow a=-b^2-b-2\)
Câu 2:
\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)
Phương trình hoành độ giao điểm:
\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)
\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b
Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)
Mặt khác do tiếp tuyến tại A và B song song
\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)
TH1: \(a=b\) thay vào (1):
\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)
TH2: \(a=4-b\)
\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)
