Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi N là trung điểm AB
\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}-\overrightarrow{MB}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MN}\right|=\left|\overrightarrow{BA}\right|\)
\(\Leftrightarrow MN=\dfrac{a^2}{2}\)
\(\Rightarrow\Delta MAB\) vuông tại M
Áp dụng BĐT AM-GM:
\(\Rightarrow MH^2=HA.HB\le\dfrac{\left(HA+HB\right)^2}{4}=\dfrac{AB^2}{4}=\dfrac{a^2}{4}\)
\(\Rightarrow MH\le\dfrac{a}{2}\)

a: 2 vecto IA+vecto IB=vecto 0
=>2 vecto IA=-vecto IB
=>I nằm giữa A và B và IA=2IB
=>vecto AI=2/3*vecto AB
b: 2/5vecto MA+3/5vecto MB
=2/5vecto MI+2/5vecto IA+3/5vecto MI+3/5vecto IB
=vetco MI+1/5(2 vecto IA+3 vecto IB)
=vecto MI

a) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AM} = \overrightarrow {MM} = \overrightarrow 0 \) (vì vectơ \(\overrightarrow {MB} = - \overrightarrow {MA} = \overrightarrow {AM} .\))
b) Xét hình bình hành BGCD ta có: \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GD} \)
\( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {DG} + \overrightarrow {GD} = \overrightarrow {{\rm{DD}}} = \overrightarrow 0 \)
(vì \(\overrightarrow {GA} = - \overrightarrow {GD} = \overrightarrow {DG} \))

Chị ơi giúp e cái này tìm 3 giá trị của x sao cho 0,6<x<0,61
Gọi I là tâm đường tròn nội tiếp tam giác ABC
\(\Rightarrow a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\)
Ta có:
\(A=\left|a\overrightarrow{MA}+b\overrightarrow{MB}+c\overrightarrow{MC}\right|=\left|\left(a+b+c\right)\overrightarrow{MI}+a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right|\)
\(=\left|\left(a+b+c\right)\overrightarrow{MI}\right|=\left(a+b+c\right).MI\)
\(Amin\Leftrightarrow MImin\)
\(\Leftrightarrow\) M trùng I

Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)


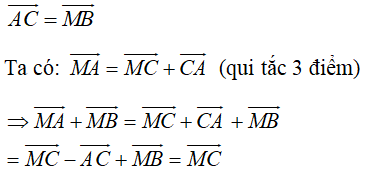
Trên đoạn AM, lấy điểm C sao cho AC = MB = 20
\(\Rightarrow\overrightarrow{AC}=\overrightarrow{MB}\)
Ta có: \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}+\overrightarrow{AC}\right|=\left|\overrightarrow{MC}\right|=MC=10\)
\(\left|\overrightarrow{MA}-\overrightarrow{MB}\right|=\left|\overrightarrow{BA}\right|=BA=50\)