Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=8cm
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
hay CB=CD
Xét ΔCBD có
DK là đường trung tuyến
CA là đường trung tuyến
DK cắt CA tại M
Do đó: M là trọng tâm
=>AM=AC/2=8/3(cm)
b: Xét ΔCAD có
G là trung điểm của AC
GQ//AD
Do đó: Q là trung điểm của CD
Vì M là trọng tâm của ΔCDB nên B,M,Q thẳng hàng

Cậu tự vẽ hình
a. Xét tg ABC có:
BC2= 102=100
AB2 + AC2= 62 + 82 = 36 + 64 = 100
=> BC2=AB2 + AC2
=> Tam giác ABC vuông tại A (định lý Py-ta-go đảo)
b. Xét △BKM và △CKD vuông tại K có:
MK chung
BK=KC (K là trung điểm BC)
=> △BKM = △CKD (2cgv)
=> BM=CM (2 cạnh tương ứng)
Xét △DMC vuông tại D và △AMB vuông tại A có:
MB=CM (cmt)
góc BMC chung
=> △DMC = △AMB (ch-gn)
=> AB=DC (2 cạnh tương ứng)

a) Ta có \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC^2=AB^2+AC^2\Rightarrow\Delta ABC\) vuông tại \(A\)
b) Xét \(\Delta BMK\) và \(\Delta CMK\) có:
\(\widehat{BKM}=\widehat{CKM}=90^0\) (gt)
\(BK=CK\) (gt)
\(KM\) chung
\(\Rightarrow\Delta BKM=\Delta CKM\) (c.g.c) \(\Rightarrow BM=CM\)
Xét \(\Delta ABM\) và \(\Delta DCM\) có:
\(\widehat{A}=\widehat{D}=90^0\)
\(MB=MC\) (đã chứng minh)
\(\widehat{AMB}=\widehat{DMC}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta ABM=\Delta DCM\) (ch-gn) \(\Rightarrow AB=DC\) (hai cạnh tương ứng)
c) Gọi \(AB\cap CD=I\)
Tam giác \(IBC\) có \(\left\{{}\begin{matrix}CA\perp BI\\BD\perp CI\\CA\cap BD=M\end{matrix}\right.\Rightarrow M\) là trực tâm tam giác \(BCI\)
\(\Rightarrow IM\perp BC\) mà \(KM\perp BC\Rightarrow I\in KM\)
Vậy \(AB,CD,KM\) đồng quy tại \(I\)

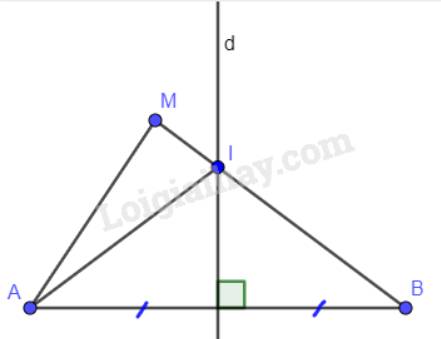
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).


Câu D d||AB bạn nhá