Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

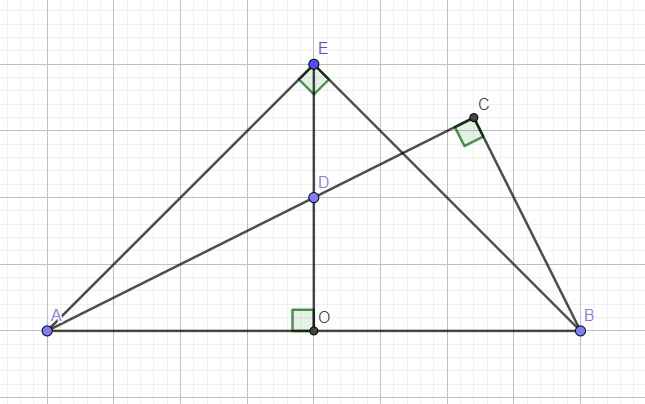
O là trung điểm AB \(\Rightarrow OA=OB=\dfrac{AB}{2}=a\)
Áp dụng định lý Pitago:
\(AD=\sqrt{AO^2+OD^2}=\dfrac{a\sqrt{5}}{2}\)
Xét hai tam giác vuông AOD và ACB có góc A chung
\(\Rightarrow\Delta AOD\sim\Delta ACB\Rightarrow\dfrac{AD}{AB}=\dfrac{AO}{AC}\Rightarrow AC=\dfrac{AO.AB}{AD}=\dfrac{4a\sqrt{5}}{5}\)
\(BC=\sqrt{AB^2-AC^2}=\dfrac{2a\sqrt{5}}{5}\)
b. Ta có: \(AE=\sqrt{AO^2+OE^2}=a\sqrt{2}\)
\(BE=\sqrt{OB^2+OE^2}=a\sqrt{2}\)
\(\Rightarrow AE^2+BE^2=4a^2=AB^2\)
\(\Rightarrow\Delta ABE\) vuông tại E (Pitago đảo)
\(\Rightarrow\) Hai điểm E và C cùng nhìn AB dưới 1 góc vuông nên bốn điểm A,B,C,E cùng thuộc đường tròn đường kính AB (đpcm)

Gọi giao điểm của AK và MB là I; giao điểm của IF với AB là J.
Xét tam giác vuông ICA ta thấy DA = DC nên DA = DC = DI.
Lại có DB là trung trực của AF nên DA = DF. Vậy thì DA = DF = DI hay tam giác IFA vuông tại F, suy ra DB // IJ.
Vậy thì DB là đường trung bình tam giác AIJ hay B là trung điểm AJ.
Ta có KF // AJ nên áp dụng Ta let ta có:
\(\frac{KM}{AB}=\frac{IM}{IB}=\frac{MF}{BJ}\)
Do AB = BJ nên KM = MF.

a: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>\(HA=HB=\dfrac{AB}{2}=2,4\left(cm\right)\)
Ta có: ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=3^2-2,4^2=3,24\)
=>\(OH=\sqrt{3,24}=1,8\left(cm\right)\)
OH+HC=OC
=>HC=OC-OH=5-1,8=3,2(cm)
b: Ta có: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(AC^2=2,4^2+3,2^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
Xét ΔAOC có \(AO^2+AC^2=OC^2\)
nên ΔAOC vuông tại A
=>CA\(\perp\)OA tại A
=>CA là tiếp tuyến của (O)
b: Xét ΔCAB có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAB cân tại C
=>CA=CB
Xét ΔOAC và ΔOBC có
OA=OB
AC=BC
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
Xét (O) có
EA,ED là các tiếp tuyến
Do đó: EA=ED
Xét (O) có
FD,FB là các tiếp tuyến
Do đó: FD=FB
Chu vi tam giác CEF là:
\(CE+EF+CF\)
=CE+ED+DF+CF
=CE+EA+CF+FB
=CA+CB
=2CA
=8(cm)