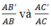Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg vuông BAC và tg vuông BHA có
\(\widehat{ACB}=\widehat{BAH}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg BAC đồng dạng với tg BHA (g.g.g)
b/ Xét tg vuông BAC có
\(BC=\sqrt{AB^2+AC^2}\) (Pitago) \(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)
\(AB^2=HB.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow HC=BC-HB=10-3,6=6,4cm\)
\(AH^2=HB.HC\) (Trong tg vuông bình phương đường cạo hạ từ đỉnh góc vuông bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH^2=3,6.6,4=23,04\Rightarrow AH=4,8cm\)
c/
Xét tg vuông HBM và tg vuông ABD có
\(\widehat{HBM}=\widehat{ABD}\left(gt\right)\) => tg HBM đồng dạng với tg ABD (g.g.g)
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{HM}{AD}\Rightarrow\dfrac{AD}{AB}=\dfrac{HM}{HB}\) (1)
Xét tg vuông ABC có BD là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (2)
Xét tg ABH có BM là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{HM}{HB}=\dfrac{AM}{AB}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{HM}{HB}=\dfrac{AM}{AB}\)
\(\Rightarrow\dfrac{AD}{AB}.\dfrac{AM}{AB}=\dfrac{CD}{BC}.\dfrac{HM}{HB}\)
Mà \(HB.BC=AB^2\) (cmt)
\(\Rightarrow\dfrac{AD.AM}{AB^2}=\dfrac{HM.CD}{AB^2}\Rightarrow AM.AD=HM.CD\)
\(\Rightarrow AM.AD-HM.CD=0\)

a:Xet ΔABC vuông tại A và ΔIBH vuông tại I có
góc B chung
=>ΔABC đồng dạng với ΔIBH
b: \(BA=\sqrt{5^2-3^2}=4\left(cm\right)\)
HB=4-1=3cm
=>HM=MB=1,5cm
ΔABC đồng dạngvơi ΔIBH
=>AB/IB=BC/BH=AC/IH
=>4/IB=5/3=3/IH
=>IB=4:5/3=12/5cm và IH=3:5/3=9/5cm

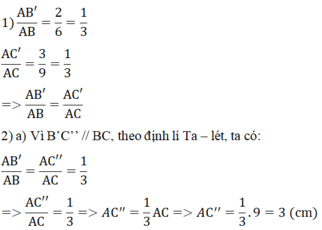
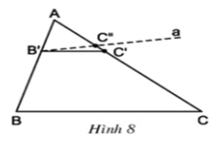
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

HN//AB
=>góc NHA=góc HAM
=>góc NHA=góc MHA
=>HA là phân giác của góc NHM
HC vuông góc HA
=>HC là phân giác ngoài của ΔIHN

a) chứng minh AH = DE
Xét tứ giác ADHE, ta có
góc HDA = góc DAE = góc AEH = 90o
nên tứ giác ADHE là hình chữ nhật
AH và DE là hai đường chéo trong hình chữ nhật ADHE nên chúng bằng nhau
b) chứng minh DIKE là hình thang vuông
* Gọi F là giao điểm của AH và DE
theo tính chất của đường chéo trong hình chữ nhật thì F là trung điểm của AH và DE, do đó tam giác FDH là tam giác cân tại F
nên góc FHD = góc FDH (1)
* DI là trung tuyến trong tam giác DBH vuông tại D nên DI = IH, do đó tam giác IDH là tam giác cân tại I
nên góc IHD = góc IDH (2)
* mặt khác góc IHD + góc FHD = góc FHI = 90o (3)
từ (1), (2), (3) suy ra góc IDH + góc FDH = góc IDF = 90o
chứng minh tương tự ta được góc FEK = 90o
tứ giác DIKE có 2 góc kề nhau là góc IDF và góc FEK đều là góc vuông nên nó là hình thang vuông.
c) tính độ dài đường trung bình của hình thang DIKE (tạm gọi là y)
y = 0.5 (ID + KE) = 0.5 (0.5 BH + 0.5 CH) = 0.25 BC
theo định lý pytago thì BC2 = AB2 + AC2 = 100 => BC = 10 => y = 2.5.
Cho mk hỏi tại sao DI là trung tuyến của tam giác vuông DBH thì tại sao mà DI lại = IH đc ?