Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét hcn AECH có AE // CH => AE // BC
Xét hcn ADBH AD // BH => AD // BC
Có : AE // BC
AD // BC
=> A, D, E thẳng hàng
b. Xét tam giác ABC có : P là tđ AB, Q là tđ AC
=> PQ là đg tb của tam giác ABC
=> PQ // BC
mà AH vuông góc BC => PQ là trung trực AH
c, Xét hcn AHBD có BA, DH là 2 đường chéo
P là tđ AB => H,P,D thẳng hàng
Tương tự => D,B,H thẳng hàng
d,Xét hcn AHBD có BA, DH là 2 đường chéo => BA = DH
Xét hcn AHCE có AC, EH là 2 đường chéo => AC= EH
hcn AHBD có : ADB = DBH = 90o
hcn AEHC có : HEC = AEC = 90o
chứng minh EDBC là hcn
=> DE = BC
Xét tam giác BAC và tam giác DAE có : AB = DH , DE = BC , HE = AC
=> tam giác BAC = tam giác DAE
=> gócBAC = gócDEH =90o
=> DH vuông góc EH
a, Ta có : \(\hept{\begin{cases}\widehat{BAD}=\widehat{ABD}\\\widehat{CAE}=\widehat{HCA}\end{cases}\Rightarrow\widehat{BAD}+\widehat{CAE}=90^o}\)
\(\widehat{BAD}+\widehat{CAE}+\widehat{BAC}=18^oC\)
=> D , A , E thẳng hàng
b, Do D là trung điểm của AB , Q là trung điểm AC
=> PQ // BC
=> PQ là trung trực của AH
c, Xét hcn ABCD , ta có :
BA , DH là 2 đường chéo
Kết hợp P là trung điểm của AB
=> D , P , H thẳng hàng
d, \(\widehat{DHE}=\widehat{DHA}+\widehat{EHA}\)
\(=\widehat{BDH}+\widehat{HEC}=90^o\)
\(\Rightarrow DH\perp EH\)

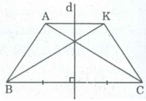
d là đường thẳng trung trực của BC nên B và C đối xứng qua d
K đối xứng với A qua d
Nên đoạn thẳng đối xứng với đoạn AB qua d là đoạn KC
Đoạn thẳng đối xứng với đoạn AC qua d là đoạn KB.

a) Đxứng với AB qua d là KC, AC qua d là KB
b) Ta có: d là trung trực nên
AK\(\perp d;BC\perp d\)
hay AK//BC
=> AKCB là hình thang
lại có AC= KB ( AC đx với KB qua d)
=> hình thang AKCB là hình thang cân
a, Đoạn thẳng đối xứng với đoạn thẳng AB qua d là KC
Đoạn thẳng đối xứng với đoạn thẳng AC qua d là KB
b, Vì d là đường trung trực của AK và BC nên AK vuông góc với d và BC vuông góc với d. Vậy AK//BC, do đó AKCB là hình thang.
Theo câu a) AC đối xứng với KB qua d, do đó AC=KB. Hình thang AKCB có 2 đường chéo bằng nhau nên là hình thang cân