Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Cho đường tròn(O) có A là điểm nằm bên ngoài đường tròn
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: OB=OC và AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC(đpcm)
b) Xét (O) có
ΔDBC nội tiếp đường tròn có DC là đường kính
nên ΔDBC vuông tại B(Định lí)
⇒DB⊥BC
Ta có: DB⊥BC(cmt)
AO⊥BC(cmt)
Do đó: DB//AO(Định lí 1 từ vuông góc tới song song)

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC

c) vì OK vg vs BC=>..............................................
d)

Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5

Xét ΔMAO vuông tại M có \(sinMAO=\dfrac{OM}{OA}=\dfrac{1}{2}\)
nên \(\widehat{MAO}=30^0\)
Xét (O) có
AM,AN là các tiếp tuyến
Do đó: AO là phân giác của góc MAN
=>\(\widehat{MAN}=2\cdot\widehat{MAO}=2\cdot30^0=60^0\)
Xét (O) có
AM,AN là các tiếp tuyến
Do đó: AM=AN
Xét ΔAMN có AM=AN và \(\widehat{MAN}=60^0\)
nên ΔAMN đều
ΔOMA vuông tại M
=>\(OM^2+MA^2=OA^2\)
=>\(MA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(MA=R\sqrt{3}\)
Chu vi tam giác AMN là:
\(AM+MN+AN=R\sqrt{3}+R\sqrt{3}+R\sqrt{3}=3R\sqrt{3}\)
ΔMAN đều
=>\(S_{AMN}=AM^2\cdot\dfrac{\sqrt{3}}{4}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\sqrt{3}\cdot R^2}{4}\)
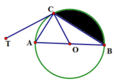
Ta có
T C A ^ = A B C ^ = 30 0 . cos A C B ^ = B C A B = 3 2 ⇒ B C = 3 c m .
Kẻ đường cao OH trong tam giác OBC. Ta có sin O B H ^ = O H O B = 1 2 ⇒ O H = 1 2 c m .
Diện tích tam giác OBC là s 1 = 1 2 . O H . B C = 3 4 c m 2 .
Ta có B O C ^ = 120 0 (vì O B C ^ = B C O ^ = 30 0 ).
Diện tích hình quạt chứa phần tô đen là s 2 = 120 360 . π . R 2 = π 3 c m 2 .
Diện tích phần tô đen là s = s 2 − s 1 = π 3 − 3 4 c m 2 .