Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

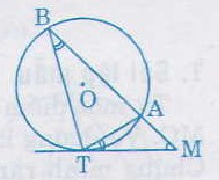
Xét hai tam giác BMT và TMA, chúng có:
chung
=
(cùng chắn cung nhỏ
![]() )
)
nên ∆BMT ~ ∆TMA, suy ra =
hay MT2 = MA. MB

Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)
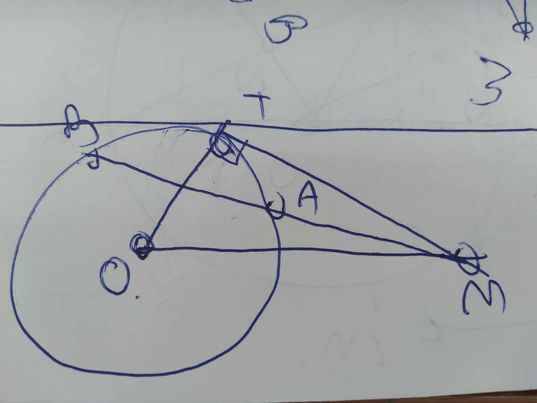

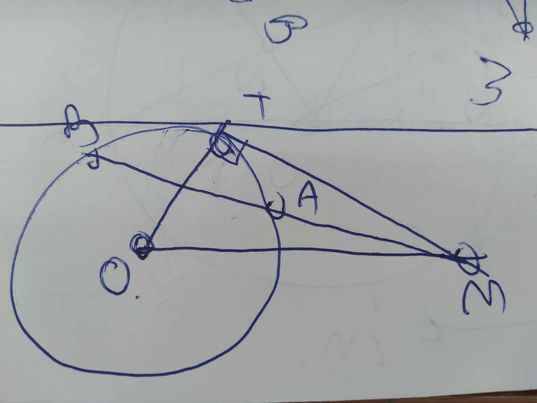
Xét ΔOTM vuông tại T có \(OM^2=OT^2+TM^2\)
=>\(TM^2=OM^2-OT^2\)
=>\(MT^2=d^2-R^2\left(1\right)\)
Xét (O) có
\(\widehat{MTA}\) là góc tạo bởi tiếp tuyến TM và dây cung TA
\(\widehat{TBA}\) là góc nội tiếp chắn cung TA
Do đó: \(\widehat{MTA}=\widehat{TBA}\)
=>\(\widehat{MTA}=\widehat{MBT}\)
Xét ΔMTA và ΔMBT có
\(\widehat{MTA}=\widehat{MBT}\)
\(\widehat{TMA}\) chung
Do đó: ΔMTA đồng dạng với ΔMBT
=>\(\dfrac{MT}{MB}=\dfrac{MA}{MT}\)
=>\(MT^2=MA\cdot MB\left(2\right)\)
Từ (1) và (2) suy ra \(MA\cdot MB=MT^2=d^2-R^2\)

Xét (O) có:
CDA và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc CDA = góc ABC hay góc MDA= gócMBC
Xét tam giác MDA và tam giác MBC có:
góc MDA = góc MBC(cmt)
góc M chung
=> 2 tam giác trên đồng dạng(g.g)
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD

a) tứ giác AOBM nội tiếp thì có tâm đường tròn là trung điểm OM
cần CM tứ giác OIMB nội tiếp: dùng tổng hai góc đối cộng với nhau bằng 180o, mà đã có OBM=90o, mà I là trung điểm dây cung CD nên OI vuông góc CD luôn => OIM=90o
Vậy tứ giác OIMB nội tiếp thì tâm đường tròn cũng tại trung điểm OM luôn
b) 5 điểm A,I,O,B,M cùng thuộc 1 đtron
=> tứ giác AIOB nội tiếp => góc AIB=AOB (cùng chắn cung)
tứ giác AIOM nội tiếp => góc AIM=AOM (ccc)
mà góc AOM=1/2AOB=AIM=1/2AIB
=> BIM=1/2AIB (đpcm

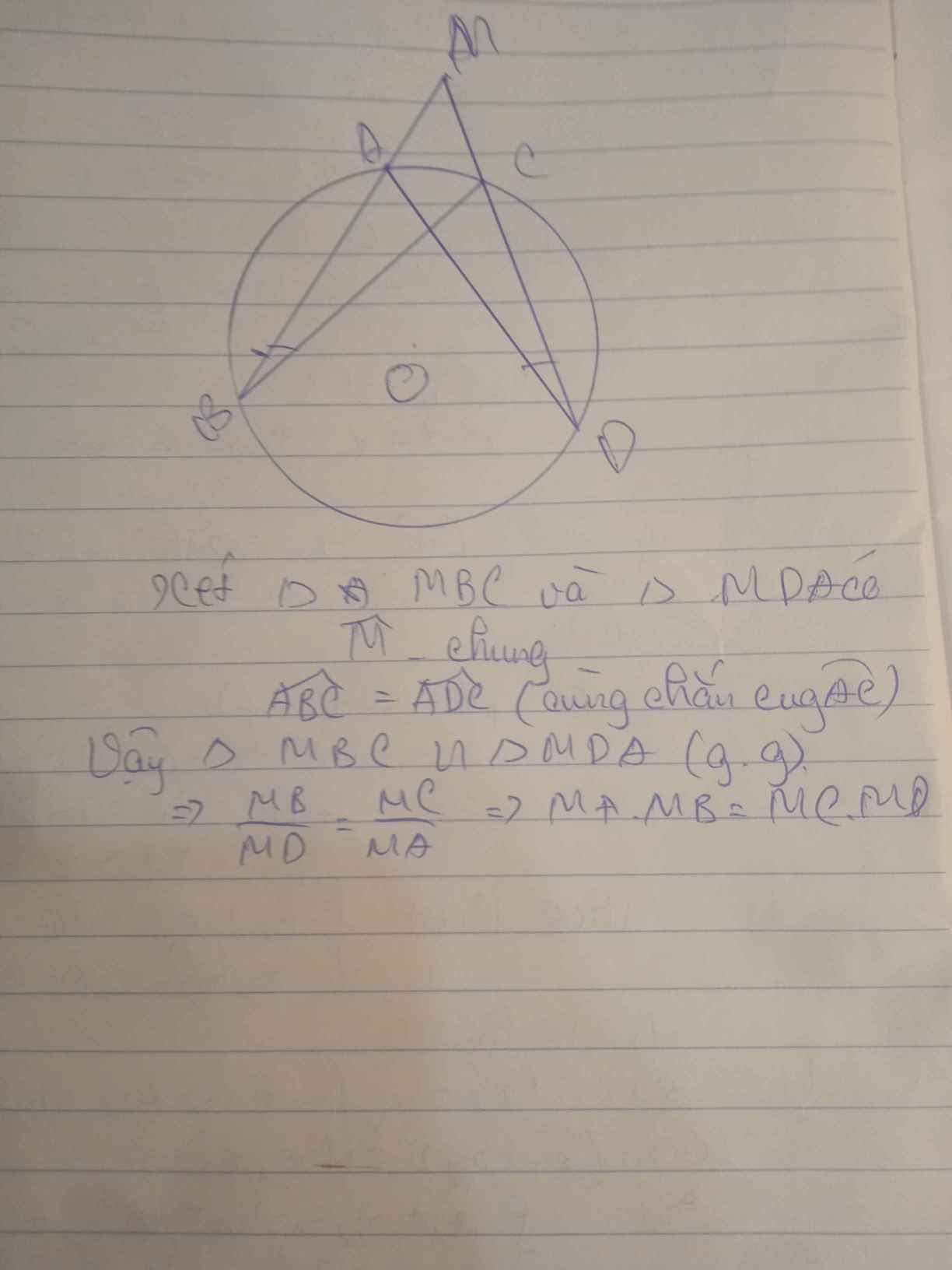

Xét đường tròn (O;R) có \(\widehat{MTA}\)là góc tạo bởi tiếp tuyến MT (tiếp điểm là T) và dây cung TA \(\Rightarrow\widehat{MTA}=\frac{1}{2}sđ\widebat{TA}\)
Mà \(\widehat{MBT}\)là góc nội tiếp chắn cung TA \(\Rightarrow\widehat{MBT}=\frac{1}{2}sđ\widebat{TA}\)
\(\Rightarrow\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}sđ\widebat{TA}\right)\)
Xét \(\Delta MTA\)và \(\Delta MBT\), ta có: \(\widehat{BMT}\)chung; \(\widehat{MTA}=\widehat{MBT}\left(cmt\right)\)
\(\Rightarrow\Delta MTA~\Delta MBT\left(g.g\right)\)\(\Rightarrow\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\)(1)
Hoàn toàn tương tự, ta có \(MT^2=MC.MD\)(2)
Vì MT là tiếp tuyến tại T của (O) \(\Rightarrow MT\perp OT\)tại T \(\Rightarrow\Delta OMT\)vuông tại T
\(\Rightarrow OM^2=MT^2+OT^2\)\(\Rightarrow MT^2=OM^2-OT^2\)
Đồng thời MT là tiếp tuyến tại T của (O;R) \(\Rightarrow OT=R\)
Như vậy ta có \(MT^2=OM^2-R^2\)(3)
Từ (1), (2) và (3) ta có đpcm.