Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

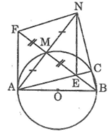
Ta có: MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: AF // NE
Mà NE ⊥ AB (chứng minh trên)
Suy ra: AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).

Em vừa giải ra, nhưng hy vọng tìm được cách đơn giản hơn.
Cách của em:
a+ b)
Dễ có AN là đường trung trực FE nên AF = FE.
^FAE=180o - 2. ^AEF = 180o - 2. ^CEB = 2. ^EBC
Dễ có BM là đường trung trực AN nên BN = BA.
Do đó tam giác NBA cân tại B.
Vậy BM là đường trung trực đồng thời là phân giác.
Vậy ^EBC = ^ABE suy ra ^FAE = 2. ^EBC = ^EBC +^ABE = ^CBA.
Ta có: ^FAB = ^FAE+^CAB=^CBA +^CAB = 90o
Vậy FA là tiếp tuyến (O) (1)
Mặt khác tứ giác FNEA có FM = ME; MN = MA nên là hình bình hành.
Vậy FA // NE (2)
Từ (1) và (2) suy ra NE vuông góc với AB.
c) BM là đường trung trực AN nên BF là đường trung trực AN
Có ngay FN = FA \(\Rightarrow\widehat{FNA}=\widehat{FAN}\)
Dễ chứng minh $\Delta MBN = \Delta MBA$ nên $\widehat{ANB}=\widehat{NAB}$
$\widehat{FNB}=\widehat{FAN}+\widehat{NAB}=\widehat{FAB}=90^o$
d) $BF^2-FN^2 =BN^2 = BM \cdot BF$
Em nghĩ quá phức tạp :D
\(\widehat{AMB}\) và \(\widehat{ACB}\) đều là góc nội tiếp chắn nửa đường tròn nên AC và BM là 2 đường cao của tam giác ABN
\(\Rightarrow\) E là trực tâm \(\Rightarrow NE\) là đường cao thứ 3 \(\Rightarrow NE\perp AB\)

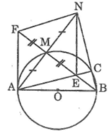
Trong tam giác ABN ta có: AN ⊥ BM và AM = MN
Suy ra tam giác ABN cân tại B
Suy ra BA = BN hay N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN (chứng minh trên)
Suy ra: FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn (B; BA)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xet ΔNAB có
AC.BM là các đường cao
AC cắt BM tại E
Do đó: E là trực tâm
=>NE vuông góc với AB
b: Xét tứ giác NEAF có
M là trung điểm chung của NA và EF
nên NEAF là hình bình hành
=>NE//AF
=>AF vuông góc với AB
=>FA là tiêp tuyến của (O)

a) Xét tam giác AMB có :
MO = OA = OB ( =bk )
\(\Rightarrow MO=\frac{1}{2}AB\)
=> Tam giác AHB vuông tại M
=> EM là đường cao của tam giác ANE
- Xét tam giác ACB có : OC = OB = OA ( =bk )
\(\Rightarrow OC=\frac{1}{2}AB\Rightarrow\Delta ACB\)vuông tại C
=> NC là đường cao của tam giác ANE
=> B là giao điểm 3 đường cao của tam giác ANE
=> AB là đường cao của tam giác ANE
Vậy : \(NE\perp AB\left(đpcm\right)\)
b) Xét 2tam giác : MAF và MNE
Có : MA = MN (gt)
MF = ME ( gt )
^AMF = ^NME ( đối đỉnh )
do đó : \(\Delta MAF=\Delta NME\left(c-g-c\right)\)
=> ^AFM = ^NEM
Mà 2 góc ^AFM và ^NEM có vị trí so le
=> AF // NE
Mà : \(NE\perp AB\)( c/m câu a ) => \(AF\perp AB\)tại A
Vậy : FA là tiếp tuyến đường tròn (O) ( đpcm )
c) Ta có : ^AMB = 90^o => \(FB\perp AN\)
MA = MB
=> FB là đường trung trực của AN
=> BN = BA ; FN = FA
- Xét 2 tam giác : ABF và NBF có : BN = BA ; FN = FA
FB chung
\(\Rightarrow\Delta ABF=\Delta NBF\left(c-c-c\right)\)
=> ^BNF = ^BAF = 90^o
\(\Rightarrow BN\perp FN\)tại B mà BN = BA
Vậy : FN là tiếp tuyến của đường tròn ( B ; BA ) ( đpcm )

a) Ta có: góc AME = 90 độ (góc nt chắn nửa đt)
=> AN vuông góc EM tại M
Mặt khác: ACN = 90 độ (góc nt chắn nửa đt)
=> AE vuông góc CN tại C
Xét tam giác ANE có : NC và EM là các đường cao
=> B là trực tâm tam giác ANE
=> AB vuông góc NE (t/c trực tâm tam giác)
b) Ta có M là trung điểm AN (t/c đối xứng)
và M cũng là trung điểm EF (t/c đói xứng)
Do đó tứ giác AENF là hính bình hành
=> FA song song NE
Mà NE vuông góc AB (cmt)
=> FA vuông góc AB tại A thuộc (O)
Vậy FA là tiếp tuyến của đt (O)
c)Ta có M là trung điểm AN (t/c đối xứng)
AN vuông góc BF tại M (góc AMB =90 độ)
=> BF là đường trung trực của AN
Xét tam giác AFB và tam giác NFB có
1/ BF cạnh chung
2/ FA = FN (t/c đ trung trực)
3/ BA = BN (t/c đ trung trực)
=> tam giác AFB = tam giác NFB
=> góc FAB = góc FNB
Mà FAB = 90 độ (cmt)
=> góc FNB bằng 90 độ
=> FN vuông góc với BN tại N thuộc (B;BN)
Mà BN = AB
=> FN là tiếp tuyến cửa đt (B;AB)
d) tam giac NBF vuong tai N co NB2=BM*BF(HE THUC LUONG trong tam giac vuong) (1)
ma NB2+NF2=BF2
=> NB2=BF2-NF2(2)
(1;2)=> BM*BF=BF2-NF2(=NB2)