Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

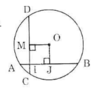
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
![]()
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.

b) Xét tam giác AHO vuông tại H có:
A O 2 = A H 2 + O H 2
⇒ AB = 2AH = 8 (cm)

Đáp án C
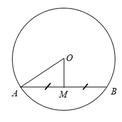
Vì M là trung điểm của AB nên ta có: 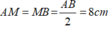
Theo quan hệ vuông góc giữa đường kính và dây ta có;
Mà khoảng cách từ O đến AM bằng 6 cm nên OM = 6 cm
Áp dụng định lí pytago vào tam giác OAM vuông ta có:
O A 2 = O M 2 + A M 2 = 6 2 + 8 2 = 100 n ê n O A = 10 c m
Suy ra: bán kính đường tròn đã cho là R = 10 cm.
Gọi `H` là tđ `AB=>AH=1/2AB=1/2 .10=5(cm)`
Xét `(O)` có: dây `AB` và `H` là tđ không đi qua tâm `O`
`=>OH \bot AB`
Xét `\triangle OHA` vuông tại `H` có:
`AH^2+OH^2=AO^2`
`=>R^2=5^2+3^2`
`=>R=\sqrt{34}(cm)`