Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)

a: góc SAO=góc SHO=90 độ
=>SAHO nội tiếp
b: Xét ΔSAB và ΔSCA có
góc SAB=góc SCA
góc ASB chung
=>ΔSAB đồng dạng với ΔSCA
=>SA^2=SB*SC

a.
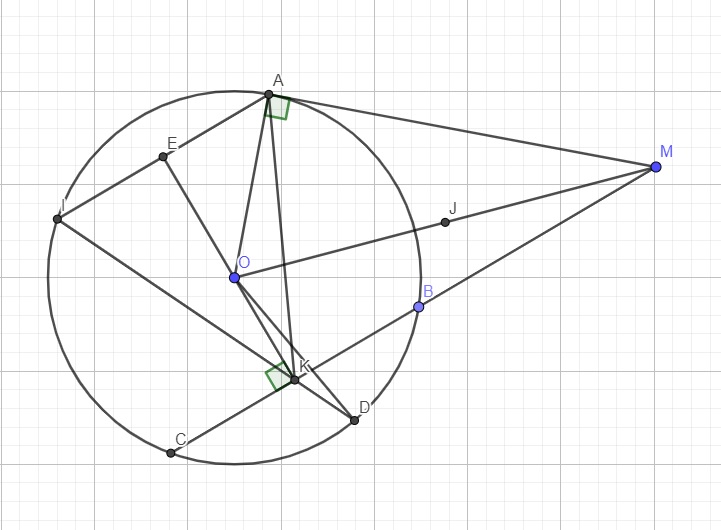
Do MA là tiếp tuyến \(\Rightarrow AM\perp OA\Rightarrow\Delta OAM\) vuông tại A
\(\Rightarrow O,A,M\) cùng thuộc đường tròn đường kính OM
Do \(OK\perp BC\Rightarrow\Delta OKM\) vuông tại K
\(\Rightarrow O,K,M\) cùng thuộc đường tròn đường kính OM
\(\Rightarrow M,A,O,K\) cùng thuộc đường tròn đường kính OM
Hay tứ giác MAOK nội tiếp đường tròn đường kính OM, với tâm là trung điểm J của OM và bán kính \(R=\dfrac{OM}{2}\)
b.
Do \(AI||BC\Rightarrow\widehat{IAK}=\widehat{AKM}\) (so le trong)
Lại có MAOK nội tiếp \(\Rightarrow\widehat{AKM}=\widehat{AOM}\) (cùng chắn cung AM)
\(\Rightarrow\widehat{IAK}=\widehat{AOM}\) (1)
Mà \(\widehat{AOM}+\widehat{AMO}=90^0\) (\(\Delta OAM\) vuông tại A theo c/m câu a)
\(\Rightarrow\widehat{IAK}+\widehat{AMO}=90^0\)
c.
Gọi E là trung điểm AI \(\Rightarrow OE\perp IA\)
Mà \(IA||BC\Rightarrow OE\perp BC\Rightarrow O,E,K\) thẳng hàng
\(\Rightarrow KE\) đồng thời là đường cao và trung tuyến trong tam giác KAI
\(\Rightarrow\Delta KAI\) cân tại K \(\Rightarrow\widehat{AIK}=\widehat{IAK}\) \(\Rightarrow\widehat{AIK}=\widehat{AOM}\) (theo (1))
Mặt khác \(\widehat{AIK}\) và \(\widehat{AOD}\) là góc nội tiếp và góc ở tâm cùng chắn cung AD của (O)
\(\Rightarrow\widehat{AIK}=\dfrac{1}{2}\widehat{AOD}\Rightarrow\widehat{AOM}=\dfrac{1}{2}\left(\widehat{AOM}+\widehat{MOD}\right)\)
\(\Rightarrow\widehat{AOM}=\widehat{MOD}\)
Xét hai tam giác AOM và DOM có:
\(\left\{{}\begin{matrix}OM\text{ chung}\\\widehat{AOM}=\widehat{MOD}\left(cmt\right)\\AO=DO=R\end{matrix}\right.\) \(\Rightarrow\Delta AOM=\Delta DOM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODM}=\widehat{OAM}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến của (O)

a) Xét tứ giác SAOB có
\(\widehat{OAS}+\widehat{OBS}=180^0\)
nên SAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔSAC và ΔSDA có
\(\widehat{SAC}=\widehat{SDA}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\)
\(\widehat{ASC}\) chung
Do đó: ΔSAC\(\sim\)ΔSDA(g-g)
Suy ra: \(\dfrac{SA}{SD}=\dfrac{SC}{SA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(SA^2=SC\cdot SD\)

a: góc MON=180-60=120 độ
b: sđ cung nhỏ MN=120 độ
=>sđ cung lớn MN=360-120=240 độ