Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác OAMC có
\(\widehat{OAM}+\widehat{OCM}=180^0\)
Do đó: OAMC là tứ giác nội tiếp

a: Xét tứ giác OACM có
\(\widehat{OAC}+\widehat{OMC}=90^0+90^0=180^0\)
=>OACM là tứ giác nội tiếp
=>O,A,C,M cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB tại M
Ta có: AM\(\perp\)MB
AM\(\perp\)OC
Do đó: OC//MB
c: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
=>KB\(\perp\)KA tại K
=>AK\(\perp\)BC tại K
Xét ΔABC vuông tại A có AK là đường cao
nên \(BK\cdot BC=BA^2=\left(2R\right)^2=4R^2\)

a, HS tự làm
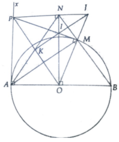
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng
a.
Do AM là tiếp tuyến của (O) \(\Rightarrow AM\perp OA\Rightarrow\widehat{OAM}=90^0\)
\(\Rightarrow\) 3 điểm O, A, M cùng thuộc đường tròn đường kính OM (1)
Tương tự, do MC là tiếp tuyến của (O) \(\Rightarrow\widehat{OCM}=90^0\)
\(\Rightarrow\) 3 điểm O, C, M cùng thuộc đường tròn đường kính OM (2)
(1);(2) \(\Rightarrow\) 4 điểm O, A, M, C cùng thuộc đường tròn đường kính OM
b.
Do M là giao điểm 2 tiếp tuyến của (O) tại A và C \(\Rightarrow MA=MC\) (t/c hai tiếp tuyến cắt nhau)
Lại có \(OA=OC=R\)
\(\Rightarrow OM\) là trung trực của AC
\(\Rightarrow OM\perp AC\) tại I
c.
Do AB là đường kính và D thuộc đường tròn \(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ADB}=90^0\) hay \(AD\perp BM\)
Áp dụng hệ thức lượng trong tam giác vuông BAM với đường cao AD:
\(AM^2=MD.MB\) (3)
Theo c/m câu b ta có \(AI\perp MO\), áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:
\(AM^2=MI.MO\) (4)
(3);(4) \(\Rightarrow MA^2=MI.MO=MD.MB\)
d.
Áp dụng hệ thức lượng trong tam giác vuông OAM với đường cao AI:
\(OA^2=OI.OM\)
Mà \(OA=OB=R\Rightarrow OB^2=OI.OM\Rightarrow\dfrac{OI}{OB}=\dfrac{OB}{OM}\)
Xét hai tam giác BOI và MOB có:
\(\left\{{}\begin{matrix}\dfrac{OI}{OB}=\dfrac{OB}{OM}\left(cmt\right)\\\widehat{MOB}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOI\sim\Delta MOB\left(c.g.c\right)\)
\(\Rightarrow\widehat{OIB}=\widehat{OBM}\)