Em làm nếu cách này sai thì bảo em làm lại cách khác nha,em mới học cách làm này.

Theo đề bài \(a\equiv1\left(mod7\right);b\equiv2\left(mod7\right)\)

\(\Rightarrow ab\equiv2\left(mod7\right)\text{ và }b^2\equiv2^2=4\left(mod7\right)\)

\(\Rightarrow3ab\equiv6\left(mod7\right)\text{ và }b^2\equiv4\left(mod7\right)\)

Do đó \(\frac{3ab-b^2}{7}\equiv\frac{6-4}{7}\equiv\frac{2}{7}\equiv2\) (mod7)

Em cảm ơn ạ

Gọi số tự nhiên lớn hơn là x đk x€N

Vì hai số ho2n kém nhau 5 đv nên số tự nhiên nhỏ hơn là x-5

Do hiệu hai bình phương của chúng bằng 125 nên ta có pt

X²-(x-5)²=125

<=>x²-x²+10x-25=125

<=>10x=150

<=>x=15

=>số tự nhiên còn lại là: 15-5=10

Theo bài ra t có PT :

\(\left\{{}\begin{matrix}x-y=5\\x^2-y^2=125\end{matrix}\right.\)

=> \(\left\{{}\begin{matrix}x=5+y\left(1\right)\\x^2-y^2=125\left(2\right)\end{matrix}\right.\)

Thay (1) vào (2) ta có :

\(\left(5+y\right)^2-y^2=125\)

=> \(y=10\left(3\right)\)

Thay (3) vào (1) ta có :

\(x=5+10=15\)

Vậy \(\left(x;y\right)\in\left\{15;10\right\}\)

2 câu tương tự nhau nên t làm 1 câu thôi

\(\left(4x-3\right).\left(4x+3\right)-\left(2x-3\right)^2=-18\)

\(\Leftrightarrow16x^2-9-4x^2+12x-9+18=0\)

\(\Leftrightarrow12x^2+12x=0\)

\(\Leftrightarrow12x.\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}12x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

Vậy...

Biến đổi A ta được :

\(A=x\left(x+11\right)\left(x+3\right)\left(x+8\right)+144\)

\(=\left(x^2+11x\right)\left(x^2+11x+24\right)+144\)

\(=\left(x^2+11x\right)^2+24\left(x^2+11x\right)+144\)

\(=\left(x^2+11x\right)^2+2.12.\left(x^2+11x\right)+12^2\)

\(=\left(x^2+11x+12\right)^2\) là một số chính phương \(\forall x\in Z\)

Vậy A là một số chính phương (đpcm)

Xin cảm ơn ạ.

Ta có

a/3x^2y/3xy =3xy.x/3xy=x/2y^2

b/Ta có

x^2+2x/3x+6=x(x+2)/3(x+2)=x/3

c/Ta có

3x+3/3x = 3(x+1)/3x=x+1/x

-Vân đúng

g: \(x\left(x-5\right)-3\left(x-5\right)=\left(x-5\right)\left(x-3\right)\)

h: \(x\left(x-y\right)-2\left(y-x\right)=\left(x-y\right)\left(x+2\right)\)

i: \(x\left(x+3\right)+5\left(x+3\right)=\left(x+3\right)\left(x+5\right)\)

k: \(m\left(x-3\right)-n\left(x-3\right)=\left(x-3\right)\left(m-n\right)\)

l: \(5x-10=5\left(x-2\right)\)

\(a)5m-5n=5(m-n)\\b) -2x-2y=-2(x+y)\\c)-7+7y=-7(1-y)\\d)10x^3-15x^2=5x^2(2x-3)\\e) x^2-xy=x(x-y)\\f)9x^4-6x^2=3x^2(3x^2-2)\\g)x(x-5)-3(x-5)=(x-3)(x-5)\\h)x(x-y)-2(y-x)=x(x-y)+2(x-y)=(x+2)(x-y)\\i)x(x+3)+5(3+x)=(x+5)(x+3)\\k)m(x-3)+n(3-x)=m(x-3)-n(x-3)=(m-n)(x-3)\\l)5x-10=5(x-2) \)

a.

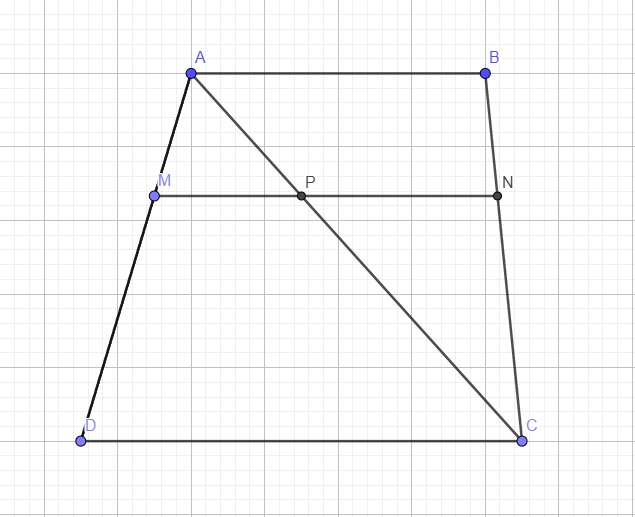
Trong \(\Delta ADC\) do \(CD||MN\) hay \(CD||MP\), áp dụng định lý Talet:

\(\dfrac{AM}{MD}=\dfrac{AP}{PC}\) (1)

Tương tự, trong \(\Delta ABC\) do \(AB||PN\) nên: \(\dfrac{AP}{PC}=\dfrac{BN}{NC}\) (2)

(1);(2) \(\Rightarrow\dfrac{AM}{MD}=\dfrac{BN}{NC}\)

b.

Ta có: \(MD=2MA\Rightarrow AD-MA=2MA\Rightarrow AD=3MA\Rightarrow\dfrac{MA}{AD}=\dfrac{1}{3}\)

Áp dụng định lý Talet trong tam giác ACD:

\(\dfrac{MA}{AD}=\dfrac{MP}{CD}=\dfrac{1}{3}\Rightarrow MP=\dfrac{CD}{3}=\dfrac{6}{3}=2\left(cm\right)\)

Lại có: \(\dfrac{BN}{NC}=\dfrac{AM}{MD}=\dfrac{1}{2}\Leftrightarrow NC=2BN\Rightarrow NC=2\left(BC-NC\right)\)

\(\Rightarrow3NC=2BC\Rightarrow\dfrac{NC}{BC}=\dfrac{2}{3}\)

Áp dụng định lý Talet cho tam giác ABC:

\(\dfrac{PN}{AB}=\dfrac{BC}{BC}=\dfrac{2}{3}\Rightarrow PN=\dfrac{2}{3}AB=\dfrac{8}{3}\left(cm\right)\)

\(\Rightarrow MN=MP+PN=\dfrac{14}{3}\left(cm\right)\)