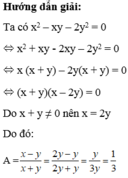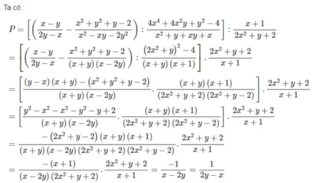Bạn tham khảo bài này nha

Link:https://olm.vn/hoi-dap/detail/266831819020.html

Chúc bạn học tốt

\(A=\left(x-y\right)\left(x^2-xy\right)-x\left(x^2+2y^2\right)\)

\(=x^3-x^2y-x^2y+xy^2-x^3-2xy^2\)

\(=-2x^2y-xy^2\)

\(=-2\cdot2^2\cdot\left(-3\right)-2\cdot\left(-3\right)^2\)

\(=8\cdot3-2\cdot9\)

=6

Thay x = -1,76; y = 3/25

⇒ P = 1/2

Ta có: \(x^2-2y^2=xy\)

\(\Leftrightarrow x^2-xy-2y^2=0\)

\(\Leftrightarrow x^2-2xy+xy-2y^2=0\)

\(\Leftrightarrow x\left(x-2y\right)+y\left(x-2y\right)=0\)

\(\Leftrightarrow\left(x-2y\right)\left(x+y\right)=0\)

Vì \(x+y\ne0\) nên x-2y=0

hay x=2y

Thay x=2y vào biểu thức \(A=\dfrac{x-y}{x+y}\), ta được: 

\(A=\dfrac{2y-y}{2y+y}=\dfrac{y}{3y}=\dfrac{1}{3}\)

Vậy: \(A=\dfrac{1}{3}\)

chs bb ak

Ta có: \(x^2-2y^2=xy\)

\(\Leftrightarrow x^2-y^2-y^2-xy=0\)

\(\Leftrightarrow\left(x-y\right)\left(x+y\right)-y\left(x+y\right)=0\)

\(\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)

Mà \(x+y\ne0\)

\(\Rightarrow x-2y=0\)

\(\Rightarrow x=2y\)

\(\Rightarrow P=\frac{2y-y}{2y+y}=\frac{y}{3y}=\frac{1}{3}\)

Từ đề bài \(\Rightarrow\)\(x^2-2y^2-xy=0\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)

Mà \(x+y\ne0\Rightarrow x-2y=0\Rightarrow x=2y\)

\(\Rightarrow P=\frac{2y-y}{2y+y}=\frac{1}{3}\)

Vì \(x^2-2y^2=xy\) 

\(\Leftrightarrow x^2-xy-y^2=0\)

\(\Leftrightarrow\left(x-y\right)^2-y\left(x+y\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left(x+y\right)-y\left(x+y\right)=0\)

\(\Leftrightarrow\left(x+y\right)\left(x-2y\right)=0\)

Theo đề bài thì có : 

\(x+y\ne0\)

\(\Rightarrow x-2y=0\)

\(\Leftrightarrow x=2y\)

Từ đó ta lại có :

\(P=\frac{2y-y}{2y+y}=\frac{y}{3y}=\frac{1}{3}\)

Vậy .......