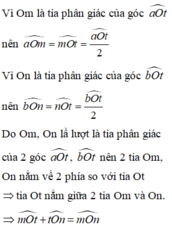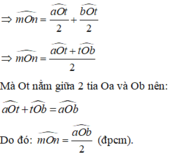Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tia ON là phân giác của góc AOB suy ra \(\widehat{AON}=\widehat{NOB}=\frac{\widehat{AOB}}{2}\)(1)
LẠi có OM nằm giữa hai tia OB và ON suy ra góc NOM + góc MOB = góc BON (2)
Suy ra OM nằm giữa OB và OA
suy ra góc AOM + góc MOB = góc AOB (3)
Từ (1), (2) và (3) suy ra góc AOM + góc BOM = 2. (góc MON + góc MOB)
góc AOM + góc BOM = 2. góc MON + 2.góc MOB
suy ra góc AOM - góc BOM = 2. góc MON
Vì ON là phân giác của AOB suy ra \(AON=NOB=\frac{AOB}{2}\)
lại có OM nằm giữa hai tia OM và ON suy ra BOM + MON = BON (1)
suy ra OM nằm giữa OB và OA
nên BOM + MOA = AOB (2)
Từ (1) và (2) suy ra AOM >BOM
suy ra \(\frac{AOM}{2}+\frac{BOM}{2}=MON+MOB\) (3)
từ (3) suy ra \(\frac{AOM}{2}-\frac{BOM}{2}=MON\)
\(=\frac{AOM-BOM}{2}\) (Đpcm)
Cậu tự thêm các kí hiệu góc vào nhé .

tớ làm thế này hk bít có đúng ko:
vì ON là tia phân giác=>ON là tia nằm giữa hai tia OA và OB; OAN=NOB=1/2AOB
vì OM nằm giữa OB và ON
mà ON thuộc AOM => OM nằm giữa hai tia OA và OB
=>AOM + MOB= AOB
=> 2MON + MOB= AOB
2MON= AOB-MOB
Vậy MON= AOB-MOB/2

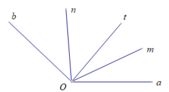
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)