Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không thể bằng nhau được bạn ạ mà chỉ xảy ra TH đồng dạng vì đâu có cặp cạnh nào bằng nhau cho trước sẵn đâu
\(\hept{\begin{cases}OA\ne OB\\OD\ne OC\end{cases}}\)
Mik nghĩ cần bổ sung thêm OB=OA.
Xét tam giác OAC và OBD có:OA=OB,^OBD=^OAC,^AOB chung
Khi đó \(\Delta\)OAC=\(\Delta\)OBD ( ch-gn ) => AC=BD

Gỉa sử đường trung trực của OA cắt OA tại H; đường trung trực của OB cắt OB tại K
Vì HI là đường trung trực của OA nên IO = IA (tính chất đường trung trực của đoạn thẳng)
Vì KI là đường trung trực của OB nên IO = IB (tính chất đường trung trực của đoạn thẳng)
b: Xet ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
góc O chung
=>ΔOAE=ΔOBF
=>OE=OF
a: 

a, xét tam giác AOE và tam giác BOF có :
OA = OB (gt)
\(\widehat{A}=\widehat{B}=90^0\)
\(\widehat{O}\)là góc chung
suy ra : tam giác AOE = tam giác BOF
suy ra : AE = BF ( cạnh tương ứng )
Hình tự vẽ nha
a)Xét tam giác AEO vuông tại A và tam giác BFO vuông tại B có :
-\(\widehat{O}\)là góc chung
-OA=OB ( GT )
=> Tam giác AEO = Tam giác BFO ( cạnh góc vuông và góc nhọn kề )
=>AE=BF ( tương ứng )
b)Vì tam giác AEO = tam giác BFO ( CM trên )
=>OF=OE ( tương ứng )
\(\widehat{ÒFB}=\widehat{OEA}\)( tương ứng )
Ta có : OB+BE=OE
OA+AF=OF
mà OF=OE ; OA=OA
=>AF=BE
Xét tam giác AFI vuông tại A và tam giác BEI vuông tại B ta có :
BE=AF ( CM trên )
\(\widehat{ÒFB}=\widehat{OEA}\)( CM trên )
=> Tam giác AFI = tam giác BEI ( cạnh góc vuông và góc nhọn kề )
c) Vì tam giác AFI = tam giác BEI ( CM trên )
=>BI=AI ( tương ứng )
Xét tam giác AOI và tam giác BOI có
OA=OB (GT)
OI là cạnh chung
BI=AI ( CM trên )
=> tam giác AOI = tam giác BOI (c.c.c)
=>\(\widehat{AOI}=\widehat{BOI}\)( tương ứng )
=> OI là tia phân giác của \(\widehat{AOB}\)

a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOB}\) chung
Do đó: ΔOAM=ΔOBN
=>\(\widehat{OMA}=\widehat{ONB}\) và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
\(\widehat{KNA}=\widehat{KMB}\)
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>\(\widehat{AOK}=\widehat{BOK}\)
=>OK là phân giác của \(\widehat{AOB}\)

a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
chung
Do đó: ΔOAM=ΔOBN
=> và OM=ON
Ta có: OA+AN=ON
OB+BM=OM
mà OA=OB và ON=OM
nên AN=BM
Xét ΔKAN vuông tại A và ΔKBM vuông tại B có
KA=KB
Do đó: ΔKAN=ΔKBM
b: ΔKAN=ΔKBM
=>KA=KB
Xét ΔOAK vuông tại A và ΔOBK vuông tại B có
OK chung
OA=OB
Do đó: ΔOAK=ΔOBK
=>
=>OK là phân giác của
Xin lỗi bạn, hồi nãy câu trả lời của mình bị lỗi. Giờ mình xin phép sửa lại chút nha:


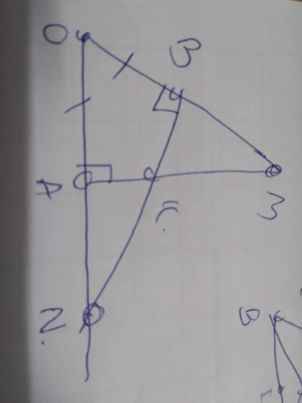

a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
\(\widehat{AOM}\) chung
Do đó: ΔOAM=ΔOBN
b: Xét ΔBMN vuông tại B và ΔANM vuông tại A có
NM chung
BN=AM
Do đó: ΔBMN=ΔANM
Suy ra: \(\widehat{IMN}=\widehat{INM}\)
hay ΔIMN cân tại I

hình bạn tự vẽ nha
có: MA⊥Ox(gt)=>△OAM vuông tại A
MB⊥Oy(gt)=>△OBM vuông tại B
xét △ vuông OAM và △vuông OBM có:
OA=OB(gt)
OM chung
=> △ vuông OAM = △vuông OBM ( cạnh huyền cạnh góc vuông )
=> AM=BM( 2 cạnh tương ứng )
=> M thuộc đường trung trực của AB
mà OA=OB(gt)=> O thuộc đường trung trực của AB
=> OM là đường trung trực của AB hay OM⊥AB
trong △ OAB có:
AC⊥OB=> AC là đường cao thứ nhất của △ OAB
BD⊥OA=> BD là đường cao thứ hai của △ OAB
OM⊥AB=> OM là đường cao thứ ba của △ OAB
=> AC,BD, OM đồng quy tại 1 điểm
vẽ hình hả bạn?