Câu hỏi của Song Ngư - Toán lớp 7 - Học toán với OnlineMath

Câu hỏi của Song Ngư - Toán lớp 7 - Học toán với OnlineMath

a) Xét \(\Delta\)AOD và \(\Delta\)COB có:

OA = OC ( gt ); ^AOD = ^COB ; OD = OB ( gt )

=> \(\Delta\)AOD = \(\Delta\)COB ( c. g. c) (1)

b) OA = OC ; OB = OD 

=> AB = CD 

(1) => ^OAD = ^OCD => ^DCB = ^BAD 

Xét \(\Delta\)IAB và \(\Delta\)ICD có:

^ABI = ^CDI (  suy ra từ (1) ) ; AB = CD ; ^IAB = ^ICD ( vì ^DCB = ^BAD )

=> \(\Delta\)IAB = \(\Delta\)ICD  ( g.c.g) (2)

Xét \(\Delta\)OIB và \(\Delta\)OID có:

IB = ID ( suy ra từ  (2) ); OI chung ; OB = OD ( gt )

=> \(\Delta\)OIB = \(\Delta\)OID  ( c.c.c)

=> ^IOB = ^IOD => OI là phân giác ^BOD 

=> OI là phân giác ^xOy  (3)

c ) \(\Delta\)AOM = \(\Delta\)COM ( c.c.c) => ^AOM = ^ COM  => OM là phân giác ^AOC   => OM là phân giác ^xOy (4)

\(\Delta\)BON = \(\Delta\)DON  ( c.c.c) => ^BON= ^DON  => ON là phân giác ^BOD   => ON  là phân giác ^xOy  (5)

Từ (3); (4) ; (5) => I; M: N thẳng hàng.

sao AOD lại = COB ko cs trên giả thuyết mầ

Câu hỏi của Song Ngư - Toán lớp 7 - Học toán với OnlineMath

Ta có: ΔOIA và ΔOIC có

      OI chung

      IA = IC (chứng minh trên)

      OA = OC (giả thiết)

ΔOIA = ΔOIC (c.c.c)

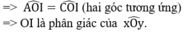
Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá

3/ (Bạn tự vẽ hình giùm)

a/ \(\Delta ABC\)và \(\Delta ADC\)có:

\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)

Cạnh AC chung

\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)

=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)

=> AD = BC (hai cạnh tương ứng)

và AB = DC (hai cạnh tương ứng)

b/ Ta có AD = BC (cm câu a)

và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)

và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)

=> AN = MC

Chứng minh tương tự, ta cũng có: BM = ND

\(\Delta AMB\)và \(\Delta CND\)có:

BM = ND (cmt)

\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)

AB = CD (\(\Delta ABC\)= \(\Delta ADC\))

=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)

=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)

và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))

=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)

=> \(\widehat{MAC}=\widehat{ACN}\)(1)

Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)

và AN = MC (cmt) (3)

=> \(\Delta MAC=\Delta NAC\)(g, c. g)

=> AM = CN (hai cạnh tương ứng) (đpcm)

c/ \(\Delta AOB\)và \(\Delta COD\)có:

\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)

AB = CD (cm câu a)

\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)

=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)

=> OA = OC (hai cạnh tương ứng)

và OB = OD (hai cạnh tương ứng)

d/ \(\Delta ONA\)và \(\Delta MOC\)có:

\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)

OA = OC (O là trung điểm AC)

\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)

=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)

=> ON = OM (hai cạnh tương ứng)

=> O là trung điểm MN

=> M, O, N thẳng hàng (đpcm)