Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAD và ΔOBC có
OA=OB
góc O chung
OD=OC
Do đó: ΔOAD=ΔOBC
=>AD=BC
b: Xét ΔEAC và ΔEBD có
góc EAC=góc EBD
AC=BD
góc ECA=góc EDB
Do đó: ΔEAC=ΔEBD

a. Ta có: OD = OB + BD; OC = OA + AC.
Mà OA = OB (gt); BD = AC (gt).
=> OD = OC.
Xét tam giác AOD và tam giác BOC có:
+ OA = OB (gt).
+ \(\widehat{O}\) chung.
+ OD = OC (cmt).
=> Tam giác AOD = Tam giác BOC (c - g - c).
=> AD = BC (Cặp cạnh tương ứng).
b. Tam giác AOD = Tam giác BOC (c - g - c).
=> \(\widehat{OAD}=\widehat{OBC}\) (2 góc tương ứng).
Mà \(\widehat{OAD}+\widehat{DAC}=180^o;\widehat{OBC}+\widehat{CBD}=180^o.\)
=> \(\widehat{DAC}=\widehat{CBD}.\)
hay \(\widehat{EAC}=\widehat{EBD}.\)
c) Tam giác AOD = Tam giác BOC (cmt).
=> \(\widehat{ODA}=\widehat{OCB}\) (2 góc tương ứng).
Xét tam giác EBD và tam giác EAC:
+ \(\widehat{BDE}=\widehat{ACE}\left(\text{}\widehat{ODA}=\widehat{OCB}\right).\) (cmt).
+ BD = AC (gt).
+ \(\widehat{EBD}=\widehat{EAC}\left(cmt\right).\)
=> Tam giác EBD = Tam giác EAC (g - c - g).
=> BE = AE (2 cạnh tương ứng).
Xét tam giác OBE và tam giác OAE:
+ OB = OA (gt).
+ OE chung.
+ BE = AE (cmt).
=> Tam giác OBE = Tam giác OAE (c - c - c).
=> \(\widehat{BOE}=\widehat{AOE}\) (2 góc tương ứng).
=> OE là phân giác của \(\widehat{xOy}\left(đpcm\right).\)

Hình vẽ trên òn đây là bài làm: a) Ta có: OC=OA+AC OD=OB+BD Mà OA=OB và AC=BD (gt) =>OC=OD Xét Δ OAD và Δ OBC có: OA=OB (gt) ˆ O góc chung
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC

a:
Ta có: OC=OA+AC
OD=OB+BD
mà OA=OB và AC=BD
nên OC=OD
Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOBC
b: ta có: ΔOAD=ΔOBC
=>\(\widehat{OAD}=\widehat{OBC};\widehat{ODA}=\widehat{OCB}\)
Ta có: \(\widehat{OAD}+\widehat{DAC}=180^0\)(hai góc kề bù)
\(\widehat{OBC}+\widehat{DBC}=180^0\)(hai góc kề bù)
mà \(\widehat{OAD}=\widehat{OBC}\)
nên \(\widehat{DAC}=\widehat{DBC}\)
Xét ΔEAC và ΔEBD có
\(\widehat{EAC}=\widehat{EBD}\)
AC=BD
\(\widehat{ECA}=\widehat{EDB}\)
Do đó: ΔEAC=ΔEBD
c: Ta có: ΔEAC=ΔEBD
=>EC=ED
Xét ΔOEC và ΔOED có
OE chung
EC=ED
OC=OD
Do đó: ΔOEC=ΔOED
=>\(\widehat{COE}=\widehat{DOE}\)
=>\(\widehat{xOE}=\widehat{yOE}\)
=>OE là phân giác của góc xOy

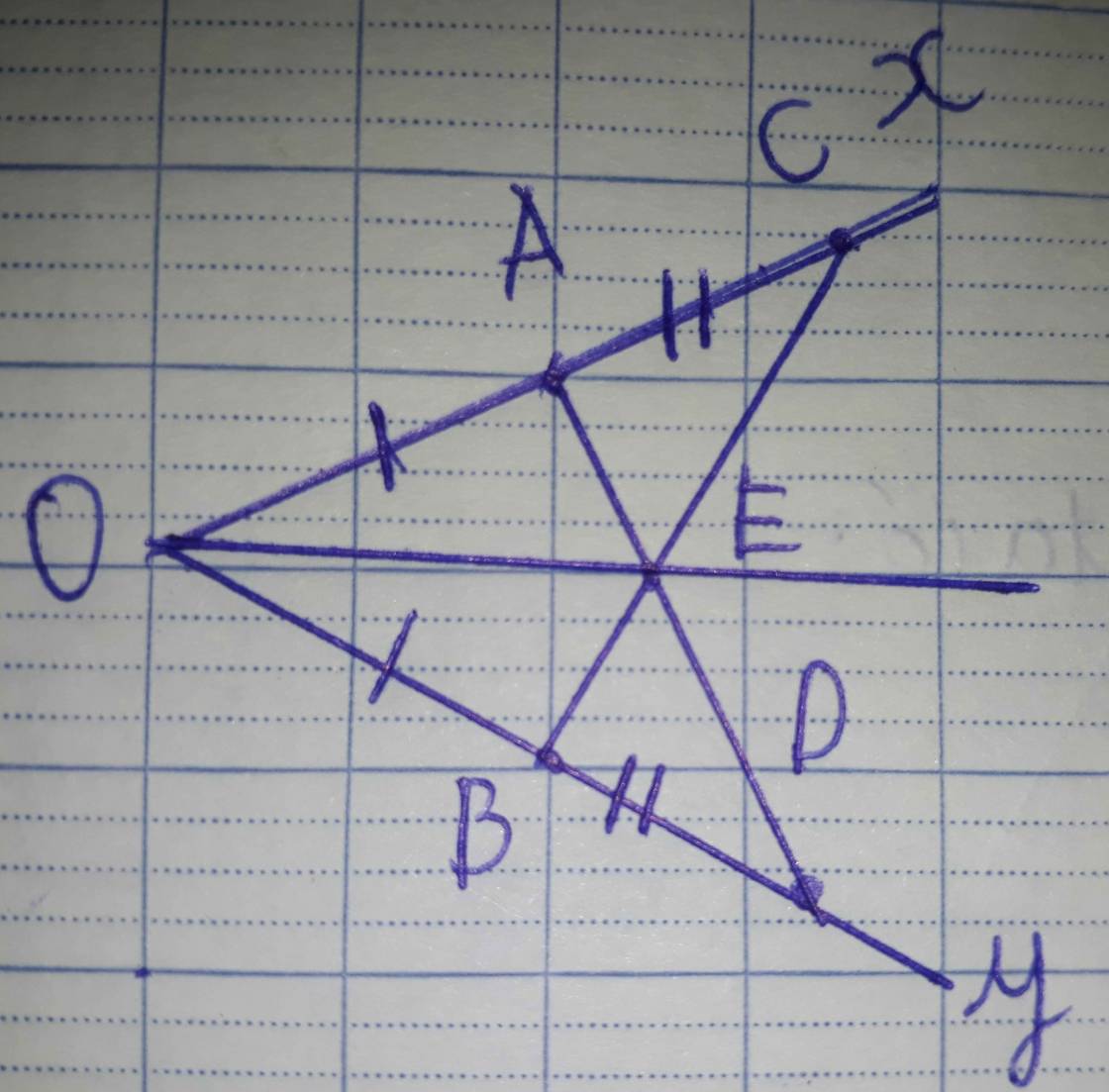
a) xét ΔOCB và ΔODA, ta có :
OA = OB (giả thiết)
\(\widehat{O}\) là góc chung
AC = BD (giả thiết)
⇒ ΔOCB = ΔODA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
b) xét ΔEAC và ΔEBD, ta có :
AD = BC (câu a)
\(\widehat{AEC}=\widehat{BED}\) (vì là 2 góc đối đỉnh)
AC = BD (giả thiết)
⇒ ΔEAC = ΔEBD (C.G.C)
c) xét ΔOAE và ΔOBE, ta có :
OA = OB (giả thiết)
AE = BE [vì ΔEAC = ΔEBD (2 cạnh tương ứng)]
OE là cạnh chung
⇒ ΔOAE = ΔOBE (c.c.c)
⇒ \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔBDC và ΔACD có
BD=AC
\(\widehat{BDC}=\widehat{ACD}\)
DC chung
Do đó: ΔBDC=ΔACD
Suy ra: \(\widehat{EAC}=\widehat{EBD}\)
Xét ΔEAC và ΔEBD có
\(\widehat{EAC}=\widehat{EBD}\)
AC=BD
\(\widehat{ECA}=\widehat{EDB}\)
Do đó: ΔEAC=ΔEBD
c: Xét ΔOEC và ΔOED có
OE chung
EC=ED
OC=OD
Do đó: ΔOEC=ΔOED
Suy ra: \(\widehat{COE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔBDC và ΔACD có
BD=AC
\(\widehat{BDC}=\widehat{ACD}\)
CD chung
Do đó: ΔBDC=ΔACD
Suy ra: \(\widehat{EBD}=\widehat{EAC}\)
Xét ΔEBD và ΔEAC có
\(\widehat{EBD}=\widehat{EAC}\)
BD=AC
\(\widehat{BED}=\widehat{AEC}\)
Do đó: ΔEBD=ΔEAC