Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

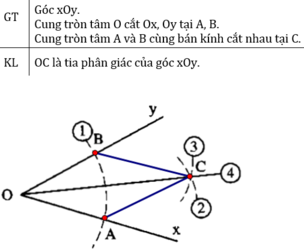
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
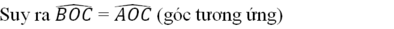
nên OC là tia phân giác của góc xOy.

\(a,\left\{{}\begin{matrix}AI=IB\left(\text{cùng là bán kính }\left(A\right);\left(B\right)\right)\\OA=OB\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.c.c\right)\\ b,\Delta AOI=\Delta BOI\\ \Rightarrow\widehat{AOI}=\widehat{BOI}\\ \Rightarrow OI\text{ là p/g }\widehat{xOy}\)

Xin lỗi bạn nhé mình không vẽ hai hình tròn đè lên nhau được nha
Điểm I nằm trên đường tròn (B, BO) nên BI = BO.
Theo giả thiết AO = BO nên:
AI =BI = AO =BO.
Hai tamm giác OAI và OBI có ba cạnh bằng nhau từng đôi một: OA = OB, AI = BI và OI chung,nên chúng bằng nhau. Ta suy ra \(\widehat{AOI}=\widehat{BOI}\)nghĩa là tia OI là tia phân giác của góc xOy.

Xét ΔCOE và ΔDOE. Ta có:
OE cạnh chung
OD = OC (giả thiết)
DE=CE ( bán kính 2 cung tròn có bán kính bằng nhau)
Suy ra: ΔCOE= ΔDOE(c.c.c)
Vậy : ∠(COE) =∠(DOE) (hai góc tương ứng)
Vì điểm E nằm trong góc xOy nên tia OE nằm giữa OC và OD (2)
Từ (1) và (2) suy ra: OE là tia phân giác của góc DOC hay OE là tia phân giác của góc xOy
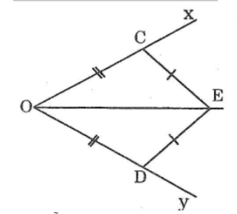
Ta có: AM = bán kính đường tròn tâm A
BM = bán kính đường tròn tâm B
Mà 2 đường tròn này có bán kính bằng nhau
Do đó, AM = BM
Xét \(\Delta \)OAM và \(\Delta \)OBM có:
OA = OB( = bán kính đường tròn tâm O)
MA = MB (cmt)
OM chung
\( \Rightarrow \) \(\Delta \)OAM = \(\Delta \)OBM ( c.c.c)
\( \Rightarrow \) \(\widehat {AOM} = \widehat {BOM}\) ( 2 góc tương ứng)
Mà OM nằm giữa 2 tia OA và OB
\( \Rightarrow \) OM là tia phân giác của góc AOB.