Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác AMN và tam giác BMN có:
MA = MB ( M thuộc đường trung trực d)
NA = NB ( N thuộc đường trung trực d)
MN là cạnh chung
vậy tam giác AMN = tam giác BMN (c.c.c)
1 đúng nhé

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)

Ta có: M nằm trên đường trung trực của AB
nên MA=MB
Ta có: N nằm trên đường trung trực của AB
nên NA=NB
XétΔAMN và ΔBMN có
MN chung
MA=MB
NA=NB
DO đó: ΔAMN=ΔBMN

Hướng dẫn:

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
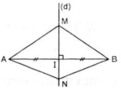
47. Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh
∆AMN = ∆BMN.
Hướng dẫn:

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)


Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Vì M, N thuộc đường trung trực của AB nên MA = MB; NA = NB
Xét tam giác AMN và tam giác BMN có:
MA = MB
NA = NB
MN chung
=> Tam giác AMN = Tam giác BMN (c.c.c)

Gọi O là giao điểm của AB và d
Vì d là đường trung trực (đtt ) của AB => Tam giác AOM = tam giác BOM ( c.g.c )
=> Tam giác AON = tam giác BOM ( c.g.c )
=> AM = BM và AN = BN, g AMN = g BMN, g ANO = g BNO hay g ANM = g BNM
Từ những điều kiện trên ta suy ra:
=> tam giác AMN = tam giác BMN ( c.c.c )
=> tam giác AMN = tam giác BMN ( c.g.c )
=> tam giác AMN = tam giác BMN ( g.c.g )
( Đây là lời giải tóm tắt của mik, bạn nhớ giải đầy đủ ra nhé )

Vì M thuộc đường trung trực của AB
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)
Do M,N nằm trên đường trung trực của đoạn AB
=>MA=MB(Tính chất đường trung trực)
NA=NB(Tính chất đường trung trực)
Xét tam giác AMN và tam giác BMN có:
MA=MB
NA=NB
MN chung
=>\(\Delta AMN=\Delta BMN\left(c.c.c\right)\left(đpcm\right)\)
cho mk hỏi (đpcm) có nghĩa là j z