Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có :
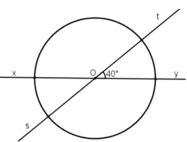
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)
a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BEFC là tứ giác nội tiếp đường tròn đường kính BC
=>B,E,F,C cùng thuộc một đường tròn
tâm I là trung điểm của BC
b: Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
=>AM\(\perp\)BC
Xét (O) có
ΔAMD nội tiếp
AD là đường kính
Do đó: ΔAMD vuông tại M
=>AM\(\perp\)MD
Ta có: AM\(\perp\)BC
AM\(\perp\)MD
Do đó: BC//MD
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(AH\(\perp\)BC)
\(\widehat{ADC}+\widehat{CAD}=90^0\)(ΔACD vuông tại C)
mà \(\widehat{ABC}=\widehat{ADC}\)
nên \(\widehat{BAH}=\widehat{CAD}\)
=>\(\widehat{BAH}+\widehat{MAD}=\widehat{CAD}+\widehat{MAD}\)
=>\(\widehat{BAD}=\widehat{CAM}\)(1)
Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn cung BD
\(\widehat{BCD}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{BAD}=\widehat{BCD}\left(2\right)\)
Xét (O) có
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CBM}=\widehat{CAM}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{CBM}=\widehat{BCD}\)
Xét tứ giác BCDM có BC//DM
nên BCDM là hình thang
Hình thang BCDM có \(\widehat{CBM}=\widehat{BCD}\)
nên BCDM là hình thang cân
c: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BA\(\perp\)BD
mà CH\(\perp\)BA
nên CH//BD
Ta có: CD\(\perp\)CA
BH\(\perp\)AC
Do đó: BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HD
=>H,I,D thẳng hàng
d: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)
nên \(\widehat{xAC}=\widehat{AFE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//Ax
Ta có: Ax//EF
Ax\(\perp\)AD
Do đó: AD\(\perp\)EF tại K
a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{AOC}=45^0\)
=>\(sđ\left(OA;OC\right)=45^0\)
b: Số đo cung AC nhỏ là:
\(sđ\stackrel\frown{AC}=45^0\)
Số đo cung AC lớn là:
3600-450=3150
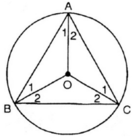
Vì tam giác ABC là tam giác đều nên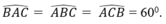 
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
* Xét tam giác AOB có:
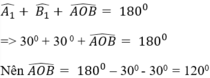
* Tượng tự ta được: 
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)
a) Ta có: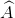 
= 
= 
= 
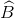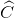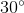(gt)
Suy ra: 
= 
= 
= 
= 
= 
= .
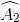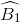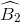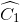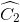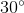Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của bà cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: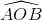 
= 
- ( +) = - 
= 
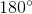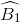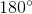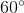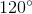
Tương tự ta suy ra =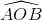 
= 
= .
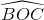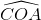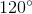b) Từ 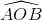= = 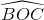= 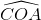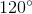ta suy ra:
Cung ABC = BCA = CAB = 240º
