Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

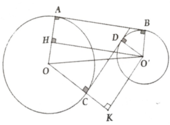
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm

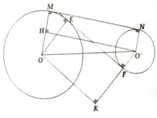
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

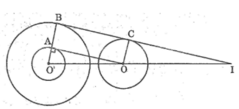
Xét tứ giác ABCO ta có:
AB // CO (gt) (1)
Mà : AB = O’B – O’A = 3 – 1 = 2 (cm)
Suy ra: AB = OC = 2 (cm) (2)
Từ (1) và (2) suy ra: ABCO là hình bình hành
Lại có: OA ⊥ O’A (tính chất tiếp tuyến)
Suy ra: BC ⊥ OC và BC ⊥ O’B
Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’)

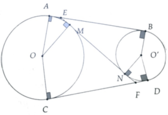
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF

