Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

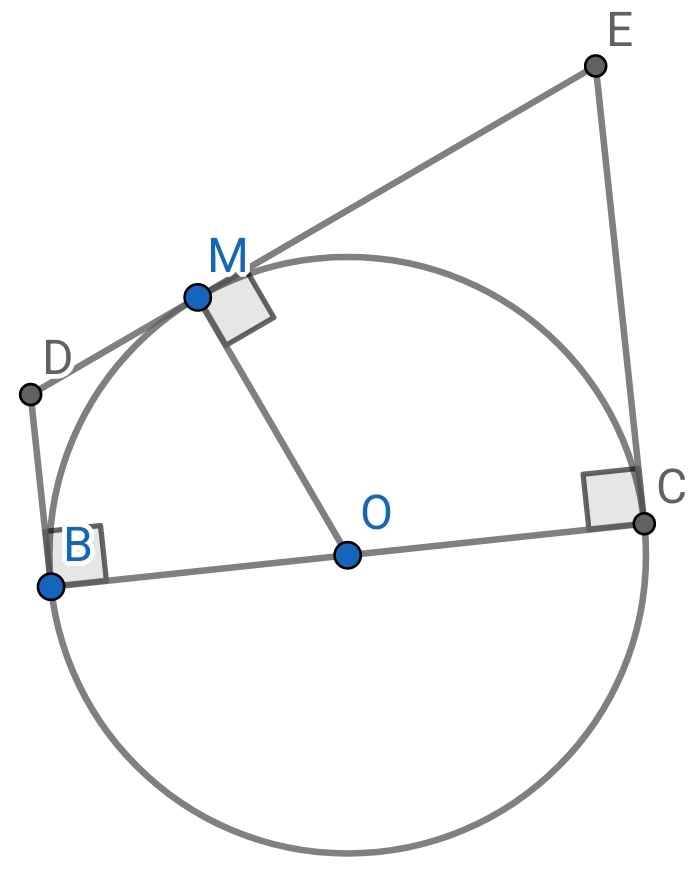 a) Do DB là tiếp tuyến tại B của (O)
a) Do DB là tiếp tuyến tại B của (O)
⇒ DB ⊥ BC (1)
Do EC là tiếp tuyến tại C của (O)
EC ⊥ BC (2)
Từ (1) và (2) ⇒ BD // CE
b) Do BD và MD là hai tiếp tuyến của (O) cắt nhau tại D
⇒ BD = MD
Do CE và ME là hai tiếp tuyến của (O) cắt nhau tại E
⇒ CE = ME
⇒ DE = MD + ME
= BD + CE

1.Cho (O;R). Qua điểm M nằm trong đương tròn vẽ các dây CD và EF không đi qua O. Tiếp tuyến tại C và D của (O) cắt nhau ở A, tiếp tuyến tại E và F của (O) cắt nhau tại B. Chứng minh OM vuông góc với AB
2. Cho (O) và đường thẳng d không cắt (O). Gọi H là hình chiếu của (O) trên d. Từ H vẽ các cát tuyến HCD và HAB với (O) (C nằm giữa H và D, A nằm giữa H và B, các cát tuyến không đi qua O). Tiếp tuyến tại A của (O) cắt d tại M. Tiếp tuyến tại C của (O) cắt d tại M. Chứng minh ΔOMN cân