Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(xOy\) và \(yOx'\) là \(hai\) góc kề bù
⇒ \(xOy+yOx'=180^0\)
Vì \(Oz'\) ⊥ \(Oz\)
⇒ \(zOz'=90^0\)
⇒ \(zOy+yOz'=90^0=\dfrac{180^0}{2}=\dfrac{xOy}{2}+\dfrac{yOx'}{2}\)
Vì \(Oz\) là \(tia\) phân giác của \(xOy\)
⇒ \(zOy=\dfrac{xOy}{2}\)
⇒ \(yOz'=\dfrac{yOx'}{2}\)
⇒ \(Oz'\)là tia phân giác của \(yOx'\)

Ta có:
\(\widehat{xOz}+\widehat{zOy}+\widehat{z'Oy}+\widehat{x'Oz'}=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}+90^o=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=90^o\)
mà \(\widehat{xOz}=\widehat{yOz}\left(gt\right)\)
nên \(\widehat{yOz}+\widehat{x'Oz'}=90^o\)(1)
mặc khác ta có:
\(\widehat{yOz}+\widehat{yOz'}=90^o\left(gt\right)\)(2)
Từ (1) và (2) suy ra:
\(\widehat{x'Oz'}=\widehat{yOz'}\)
=> Oz' là tia phân giác của \(\widehat{x'Oy}\) (đpcm)
Chúc bạn học tốt!!!
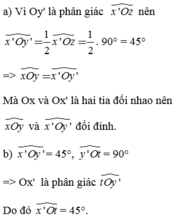
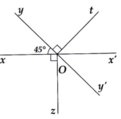
Ta có: Oz là tia phân giác của \(\widehat{xOy}\) (gt)
\(\Rightarrow\widehat{xOz}=\widehat{yOz}\)
Vì \(Oz\perp Oz'\) (gt) nên: \(\widehat{yOz}+\widehat{yOz'}=90^o\)
Lại có: \(\widehat{xOz}+\widehat{yOz}+\widehat{yOz'}+\widehat{x'Oz'}=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=180^o-\left(\widehat{yOz}+\widehat{yOz'}\right)\)
\(=180^o-90^o=90^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=\widehat{yOz}+\widehat{yOz'}=90^o\)
Mà \(\widehat{xOz}=\widehat{yOz}\) (cmt)
\(\Rightarrow\widehat{x'Oz'}=\widehat{yOz'}\)
`=>` Tia Oz' là tia phân giác của \(\widehat{x'Oy}\) (đpcm)