Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Khi đó ![]()
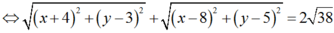
Áp dụng bất đẳng thức Bunhiakovsky ta có:

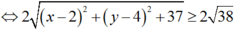
![]()
Vậy Min|z – 2 – 4i| = 1

a) (3 + 2i)z – (4 + 7i) = 2 – 5i
⇔(3+2i)z=6+2i
<=> z = \(\dfrac{\text{6 + 2 i}}{\text{3 + 2 i}}\) = \(\dfrac{22}{13}\) - \(\dfrac{6}{13}\)i
b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z
⇔(7−3i−5+4i)=−2−3i
⇔z= \(\dfrac{\text{− 2 − 3 i}}{\text{2 + i}}\) = \(\dfrac{-7}{5}\) - \(\dfrac{4}{5}i\)
c) z2 – 2z + 13 = 0
⇔ (z – 1)2 = -12 ⇔ z = 1 ± 2 √3 i
d) z4 – z2 – 6 = 0
⇔ (z2 – 3)(z2 + 2) = 0
⇔ z ∈ { √3, - √3, √2i, - √2i}

\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?

a) (3 + 4i)z = (2 + 5i) – (1 – 3i) = 1 + 8i
Vậy z=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45iz=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45i
b) (4 + 7i)z – (5 – 2i) = 6iz ⇔ (4 + 7i)z – 6iz = 5 – 2i
⇔ (4 + i)z = 5 – 2i
⇔z=5−2i4+i=(5−2i)(4−i)17⇔z=1817−1317i
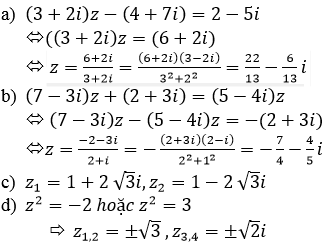
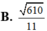

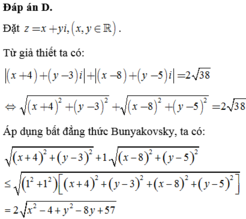
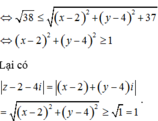

Đáp án A
z = z 1 + z 2 = 7 - 4i