Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

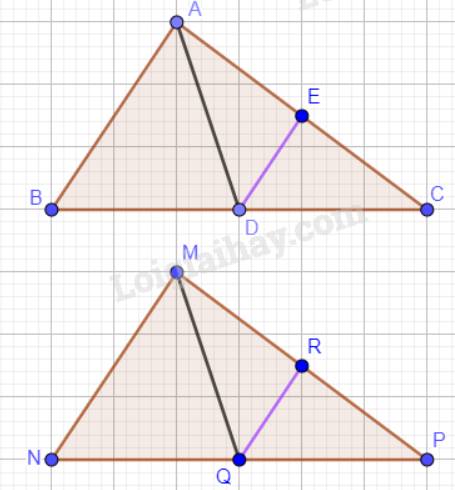
a) Xét hai tam giác ABD và tam giác MNQ:
AB = MQ (do \(\Delta ABC = \Delta MNP\)).
\(\widehat {ABD} = \widehat {MNQ}\) (\(\widehat {ABD} = \widehat {MNQ}\)).
BD = NQ (\(\dfrac{1}{2}BC = \dfrac{1}{2}NP\))
BC = NP (do \(\Delta ABC = \Delta MNP\)).
Vậy \(\Delta ABD = \Delta MNQ\)(c.g.c) nên AD = MQ ( 2 cạnh tương ứng)
b) Vì \(\Delta ABC = \Delta MNP\) nên BC = NP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}BC = \dfrac{1}{2}NP\) hay DC = QP
Vì \(\Delta ABC = \Delta MNP\) nên AC = MP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}AC = \dfrac{1}{2}MP\) hay EC = RP
Xét hai tam giác DEC và tam giác QRP:
DC = QP
\(\widehat {ECD} = \widehat {RPQ}\)(\(\Delta ABC = \Delta MNP\))
EC = RP
Vậy \(\Delta DEC = \Delta QRP\)(c.g.c) nên DE = QR ( 2 cạnh tương ứng)

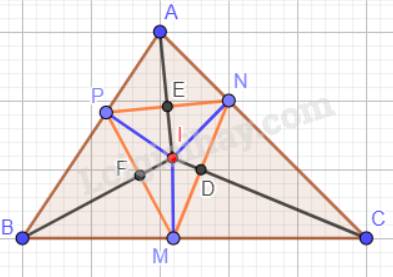
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.

B ở đâu vậy bạn ? Trong đề làm gì có nói kẻ B mà từ B đã kẻ đường vuông góc rồi ?

Bài làm:
P/s: Bạn sửa đề thành: "Trên tia đối của tia BA lấy điểm P sao cho B là trung điểm MP" nhé.
Từ N kẻ đường thẳng song song với AP cắt BC tại D
Vì ND // AP // AB
\(\Rightarrow\widehat{NDC}=\widehat{ABC}\left(1\right)\)
Mà tam giác ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\widehat{NCD}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{NCD}=\widehat{NDC}\)
=> Tam giác NDC cân tại N
=> ND = NC (3)
Mà MB = BP ( B là trung điểm MP ) (4)
Kết hợp giả thiết BM = CN với (3) và (4) ta được: ND = BP (S)
Mà ND // BP \(\Rightarrow\hept{\begin{cases}\widehat{IDN}=\widehat{IBP}\left(so.le.trong\right)\\\widehat{IPB}=\widehat{IND}\left(so.le.trong\right)\end{cases}\left(A\right)}\)
Ta có: \(\Delta IDN=\Delta IBP\left(g.c.g\right)\) vì:
\(\hept{\begin{cases}\widehat{IDN}=\widehat{IBP}\left(theo.\left(A\right)\right)\\BP=DN\left(theo.\left(S\right)\right)\\\widehat{IPB}=\widehat{IND}\left(theo.\left(A\right)\right)\end{cases}}\)
\(\Rightarrow IN=IP\)
=> I là trung điểm NP
Đoạn CM tam giác bằng nhau nó bị lỗi nên mk viết lại đoạn đấy:
+ \(\widehat{IDN}=\widehat{IBP}\left(theo\left(A\right)\right)\)
+ \(BP=DN\left(theo\left(S\right)\right)\)
+ \(\widehat{IPB}=\widehat{IND}\left(theo\left(A\right)\right)\)

a) xét \(\Delta MNP\)VUÔNG TẠI M CÓ
\(\Rightarrow NP^2=MN^2+MP^2\left(PYTAGO\right)\)
THAY\(NP^2=4^2+3^2\)
\(NP^2=16+9\)
\(NP^2=25\)
\(\Rightarrow NP=\sqrt{25}=5\left(cm\right)\)
XÉT \(\Delta MNP\)CÓ
\(\Rightarrow NP>MN>MP\left(5>4>3\right)\)
\(\Rightarrow\widehat{M}>\widehat{P}>\widehat{N}\)( QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN)
B) xét \(\Delta\text{ CPM}\)VÀ\(\Delta\text{CPA}\)CÓ
\(PM=PA\left(GT\right)\)
\(\widehat{MPC}=\widehat{APC}=90^o\)
PC LÀ CAH CHUNG
=>\(\Delta\text{ CPM}\)=\(\Delta\text{CPA}\)(C-G-C)
c)
\(\Delta CPM=\Delta CPA\left(cmt\right)\)
\(\Rightarrow\widehat{CMP}=\widehat{CPA}\left(\text{hai góc tương ứng}\right)\)
\(\text{Ta có: }\)\(\widehat{MNA}+\widehat{NAM}=90^o\left(\Delta MNA\perp\text{ tại M}\right)\)
\(\widehat{NMC}+\widehat{CMP}=90^o\)
\(\Rightarrow\widehat{MNA}+\widehat{NAM}=\)\(\widehat{NMC}+\widehat{CMP}\)
\(\Rightarrow\widehat{MNA}=\widehat{NMC}\left(\widehat{CMP}=\widehat{NAM}\right)\)
\(Hay:\)\(\widehat{MNC}=\widehat{NMC}\)
\(\Rightarrow\Delta NMC\text{ cân}\)
\(\Rightarrow CN=CM\left(đpcm\right)\)
Hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM nên \(\Delta ABC = \Delta MNP\)(c.c.c)
Suy ra: \(\widehat {ABI} = \widehat {MNK}\) ( 2 góc tương ứng).
Ta có: I, K lần lượt là trung điểm của BC và NP mà BC = NP, suy ra: \(BI = NK\).
Xét tam giác ABI và tam giác MNK có:
AB = MN;
\(\widehat {ABI} = \widehat {MNK}\);
BI = NK.
Vậy \(\Delta ABI = \Delta MNK\)(c.g.c). Suy ra: AI = MK (2 cạnh tương ứng).
Vậy AI = MK.