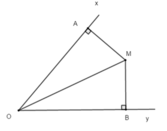
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy

Xét hai tam giác vuông OMA và OMB có:

OM là cạnh chung

MA = MB (gt)

Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)

Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)

Vậy OM là tia phân giác của  x O y ^

Vậy thứ tự sắp xếp phải là: b, c, a, d, e.

Chọn đáp án A

(Bạn tự vẽ hình giùm)

1/ \(\Delta ABC\)vuông tại A

=> \(BC^2=AB^2+AC^2\)(định lý Pitago)

=> \(BC^2=9^2+6^2\)

=> \(BC^2=9+36\)

=> \(BC^2=45\)

=> \(BC=\sqrt{45}\)(cm)

2/ Ta có: \(AE=EC=\frac{AC}{2}=\frac{6}{2}\)= 3 (cm)

\(\Delta BAD\)và \(\Delta EAD\)có: BA = EA (= 3cm)

\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác \(\widehat{A}\))

Cạnh AD chung

=> \(\Delta BAD\)= \(\Delta EAD\)(c. g. c) (đpcm)

3/ \(\Delta ABC\)và \(\Delta AME\)có: \(\widehat{A}\)chung

AB = AE (\(\Delta BAD\)= \(\Delta EAD\))

\(\widehat{ABC}=\widehat{AEM}\)(\(\Delta BAD\)= \(\Delta EAD\))

=> \(\Delta ABC\)= \(\Delta AME\)(g. c. g) => AC = AM (hai cạnh tương ứng)

nên \(\Delta ACM\)cân tại A

và \(\widehat{A}=90^o\)

=> \(\Delta ACM\)vuông cân tại A (đpcm)

4/ Ta có: \(\widehat{AEM}+\widehat{AME}=90^o\)

=> \(\widehat{AEM}< 90^o\)(vì số đo của \(\widehat{AEM}\)và \(\widehat{AME}\)luôn luôn là số dương)

=> \(\widehat{MEC}>90^o\)(tự chứng minh)

=> \(\Delta MEC\)tù => MC là cạnh lớn nhất => ME < MC

áp dụng đ/lý pitago vào tam giác v ABC ta đ̣c BC^2=AB^2+AC^2=3^2+6^2   BC=3căn5 cm                             câu b  xét tam g ABD và tam g AED ta cóAB=AE=3 cm góc BAD=góc EAD(gt) AD chung nên 2 tam g = nhau    câu c góc ABC=góc AEM(VÌgócABD=AED mà AED+AME=90 độ)   xét tam giác ABC và tg AMEcógócA chung AB=AE gócABC=AEM  nên 2 tgiác =nhau suy raAM=AC suy ra tamg AMC v cân    

a, góc ở đỉnh bảng 80o

b, góc ở đáy bằng 55o

c,số đo góc B và góc C=(180-góc A) /2

1

a) Vì trong một tam giác cân , hai góc ở đấy bằng nhau nên tổng 2 góc ở đáy của tam giác cân đó có số đo độ là :

50 + 50 = 100⁰

=> Góc ở đỉnh của tam giác cân có số đo độ là :

180⁰ - 100⁰ = 80⁰

b) Vì trong một tam giác cân , hai góc ở đấy bằng nhau nên nếu 1 góc ở đáy của tam giác đó bằng 70⁰ => góc còn lại ở đáy phải bằng 70⁰

c) Số đo góc B và góc C bằng :

( 180 - A)/2

cạnh: AB = DE ,  BC = EF ,   AC = DF

góc: A = D,  B= E,   C = F

k nhé