Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nguyễn Việt LâmTrần Trung Nguyênsaint suppapong udomkaewkanjanaNguyễn Thanh Hằngtran nguyen bao quanShurima Azir giúp mk câu a câu c nhé
a: Tọa độ giao điểm là:
2x+1=x+3 và y=x+3
=>x=2 và y=5
Thay x=2 và y=5 vào (d),ta được:
\(2\left(2m-1\right)+3=5\)
=>2m-1=1
=>2m=2
=>m=1
b: Tọa độ A là:
y=0 và x=-3/(2m-1)
=>OA=3/|2m-1|
Tọa độ B là:
x=0 và y=(2m-1)*0+3=3
=>OB=3
Theo đề, ta có: \(\dfrac{1}{2}\cdot\dfrac{3}{\left|2m-1\right|}\cdot3=3\)
=>\(\dfrac{3}{2\left|2m-1\right|}=1\)
=>2|2m-1|=3
=>2m-1=3/2 hoặc 2m-1=-3/2
=>m=5/4 hoặc m=-1/4

a:
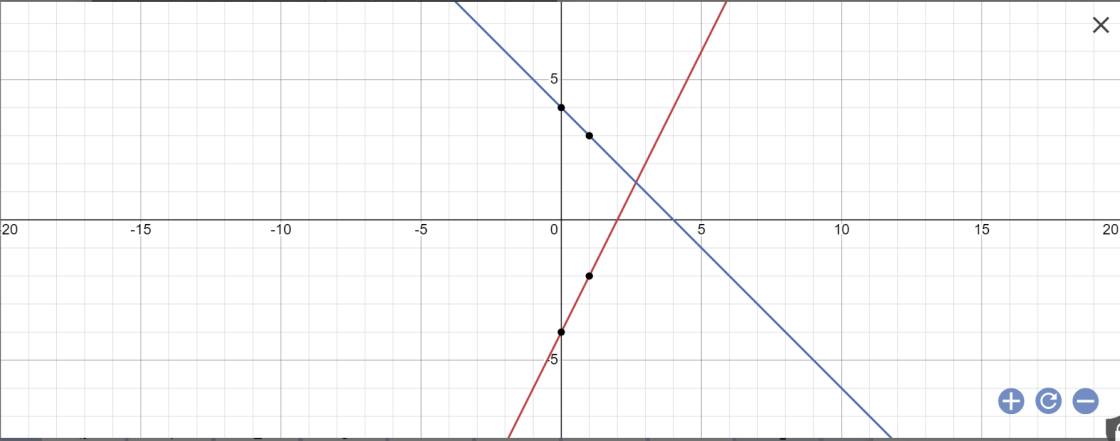
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
a: Tọa độ giao điểm là:
2x+1=x+3 và y=x+3
=>x=2 và y=5
Thay x=2 và y=5 vào (d),ta được:
\(2\left(2m-1\right)+3=5\)
=>2m-1=1
=>2m=2
=>m=1
b: Tọa độ A là:
y=0 và x=-3/(2m-1)
=>OA=3/|2m-1|
Tọa độ B là:
x=0 và y=(2m-1)*0+3=3
=>OB=3
Theo đề, ta có: \(\dfrac{1}{2}\cdot\dfrac{3}{\left|2m-1\right|}\cdot3=3\)
=>\(\dfrac{3}{2\left|2m-1\right|}=1\)
=>2|2m-1|=3
=>2m-1=3/2 hoặc 2m-1=-3/2
=>m=5/4 hoặc m=-1/4