Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn: C
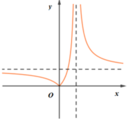
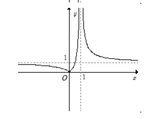
Đồ thị hàm số (A) là đồ thị của hàm số y = x x - 1
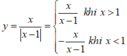
Ta giữ nguyên phần đồ thị (C) nằm phía bên phải đường thẳng x = 1 ;
lấy đối xứng phần đồ thị (C) nằm bên trái đường thẳng x = 1 qua trục hoành.
Ta được đồ thị hàm số (C).
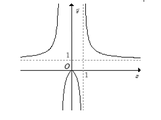
Ta có y = x x - 1 = x x - 1 k h i x > 1 - x x - 1 k h i x < 1
Do đó đồ thị hàm số y = x x - 1 được suy từ đồ thị hàm số y = x x - 1 bằng cách:
● Giữ nguyên phần đồ thị hàm số phía bên phải đường thẳng x = 1.
● Phần đồ thị hàm số
y = x x - 1
phía bên trái đường thẳng x= 1 thì lấy đối xứng qua trục hoành.
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số y = x x - 1
Chọn B.
Chọn D
Ta có
Vì f'(x) luôn đồng biến trên
ℝ
nên 
, do đó: a > 0 và b > 0
Mặt khác vì đồ thị hàm số không cắt trục Ox nên chọn đáp án D.
Chọn A.
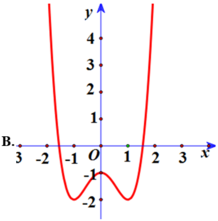
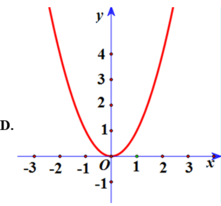
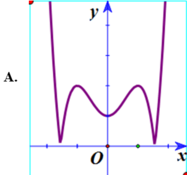
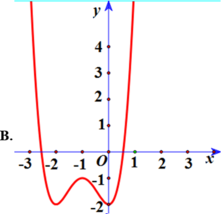
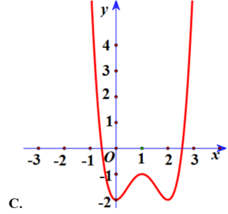
Vẽ đồ thị y = x 4 - 2 x 2 - 1 . Giữ nguyên phần đồ thị trên O x , phần dưới Ox thì lấy đối xứng qua O x ta được đồ thị cần vẽ
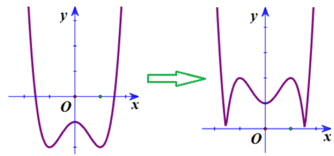
Chọn A.
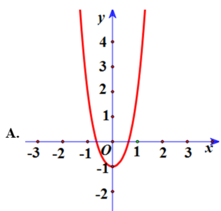
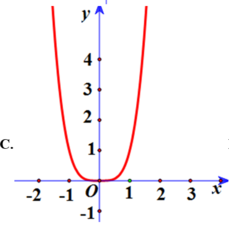
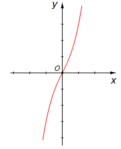
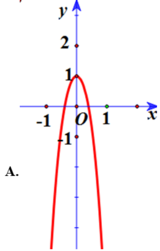
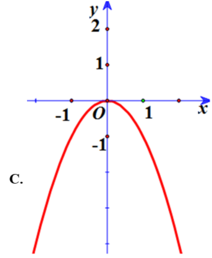
Hàm số qua 0 ; - 1 do đó loại B, C. Do a > 0 nên đồ thị hướng lên suy ra đáp án A.
Chọn A.
Do a < 0 , b < 0 nên đồ thị hướng xuống và chỉ có 1 cực trị nên loại B, D.
Hàm số qua 0 ; 1 nên loại C.
Đáp án C
Phương trình hoành độ giao điểm của (C) và d là:
(*)
(C) cắt d tại hai điểm phân biệt 
có hai nghiệm phân biệt x1, x2
Gọi 
và 
là các giao điểm của (C) và d với 
Khi đó
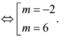
Ngoài ra, ta có thể kiểm tra sau khi có 
Khi đó, ta loại các phương án m = 1; m = 5
Thử một phương án m = -2, ta được phương trình:
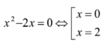
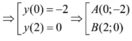
Chọn A.
Hướng dẫn giải:
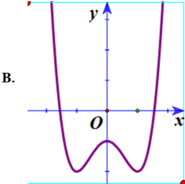
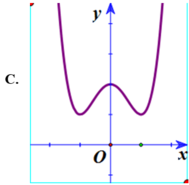
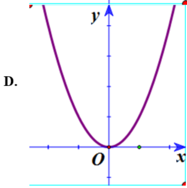
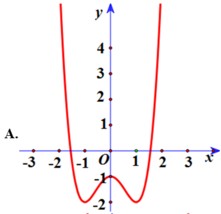
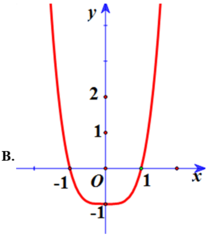
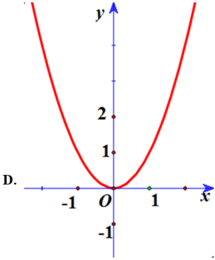
Do a > 0, b > 0 nên hàm số chỉ có 1 cực tiểu, suy ra loại B
Hàm số qua (1; 2) nên loại C, D.