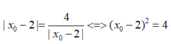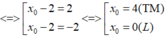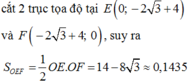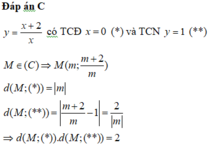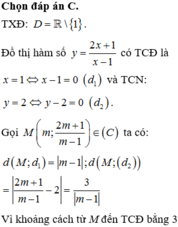Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Vì I là tâm đối xứng của đồ thị C ⇒ I 2 ; 2
Gọi M x 0 ; 2 x 0 − 1 x 0 − 2 ∈ C ⇒ y ' x 0 = − 3 x 0 − 2 2 suy ra phương trình tiếp tuyến Δ là
y − y 0 = y ' x 0 x − x 0 ⇔ y − 2 x 0 − 1 x 0 − 2 = − 3 x 0 − 2 2 x − x 0 ⇔ y = − 3 x 0 − 2 2 + 2 x 0 2 − 2 x 0 + 2 x 0 − 2 2
Đường thẳng Δ cắt TCĐ tại A 2 ; y A → y A = 2 x 0 + 2 x 0 − 2 ⇒ A 2 ; 2 x 0 + 2 x 0 − 2
Đường thẳng Δ cắt TCN tại B x B ; 2 → x B = 2 x 0 − 2 ⇒ B 2 x 0 − 2 ; 2
Suy ra I A = 6 x 0 − 2 ; I B = 2 x 0 − 2 → I A . I B = 6 x 0 − 2 .2 x 0 − 2 = 12
Tam giác IAB vuông tại I ⇒ R Δ I A B = A B 2 = I A 2 + I B 2 2 ≥ 2 I A . I B 2 = 6
Dấu bằng xảy ra khi và chỉ khi I A = I B ⇔ 3 = x 0 − 2 2 ⇔ x 0 = 2 + 3 x 0 = 2 − 3
Suy ra phương trình đường thẳng Δ và gọi M, N lần lượt là giao điểm của Δ với Ox, Oy
Khi đó M 2 x 0 2 − 2 x 0 + 2 3 ; 0 , N 0 ; 2 x 0 2 − 2 x 0 + 2 3 ⇒ S Δ O M N = 1 2 O M . O N
Vậy S m a x = 14 + 8 3 ≈ 27 , 85 ∈ 27 ; 28 k h i x 0 = 2 + 3
Đáp án C
Phương pháp: Xác định các đường tiệm cận của đồ thị hàm số.
Gọi điểm M thuộc đồ thị hàm số (C), tính khoảng cách từ M đến các đường tiệm cận và sử dụng BĐT Cauchy tìm GTNN của biểu thức đó từ đó suy ra tọa độ các điểm M, N.
Tính độ dài MN.
Cách giải: TXĐ: D = R\ {3}
Đồ thị hàm số có đường TCN y = 4 (d1) và TCĐ x = 3 (d2).
Gọi điểm M
∈
(C) có dạng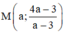 
khi đó ta có:
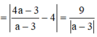
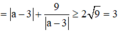
Dấu = xảy ra
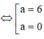
Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách= a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)