Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Học sinh tự làm.
b) 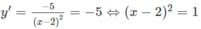
Ta có: y(1) = -3 , y(3) = 7
Từ đó ta có hai phương trình tiếp tuyến phải tìm là:
y + 3 = −5(x – 1) ⇔ y = −5x + 2
y – 7 = −5(x – 3) ⇔ y = −5x + 22

a) Học sinh tự làm
b) Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10

Ta có: y′ = –4 x 3 – 2x
Vì tiếp tuyến vuông góc với đường thẳng y = x/6 – 1 nên tiếp tuyến có hệ số góc là –6. Vì vậy:
–4 x 3 – 2x = –6
⇔ 2 x 3 + x – 3 = 0
⇔ 2( x 3 – 1) + (x – 1) = 0
⇔ (x – 1)(2 x 2 + 2x + 3) = 0
⇔ x = 1(2 x 2 + 2x + 3 > 0, ∀ x)
Ta có: y(1) = 4
Phương trình phải tìm là: y – 4 = -6(x – 1) ⇔ y = -6x + 10

Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm
Ta có: y' \(=\dfrac{-3}{\left(x+1\right)^2}\)
k=f'\(\left(x_0\right)\)\(\Rightarrow-3=\dfrac{-3}{\left(x_0+1\right)^2}\Leftrightarrow\left(x_0+1\right)^2=1\)\(\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-2\end{matrix}\right.\)
Với \(x_0=0\) ta có pt tiếp tuyến:
\(d:3x+y-2=0\)
Với \(x_0=-2\) ta có pt tiếp tuyến:
\(d:3x+y+10=0\)
a: Tọa độ giao điểm của (d) với trục Ox là:
y=0 và (-x+2)=0
=>x=2 và y=0
\(y'=\dfrac{\left(-x+2\right)'\left(x+1\right)-\left(-x+2\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{\left(-\left(x+1\right)+x-2\right)}{\left(x+1\right)^2}=\dfrac{-3}{\left(x+1\right)^2}\)
Khi x=2 thì y'=-3/(2+1)^2=-3/9=-1/3
y-f(x0)=f'(x0)(x-x0)
=>y-0=-1/3(x-2)
=>y=-1/3x+2/3
b: Tọa độ giao của (d) với trục Oy là;
x=0 và y=(-0+2)/(0+1)=2
Khi x=0 thì \(y'=\dfrac{-3}{\left(0+1\right)^2}=-3\)
y-f(x0)=f'(x0)(x-x0)
=>y-2=-3(x-0)
=>y=-3x+2

\(y'=\dfrac{3}{\left(x+1\right)^2}\)
Gọi \(M\left(m;\dfrac{2m-1}{m+1}\right)\) là tiếp điểm
Phương trình tiếp tuyến tại M:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{2m-1}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+2m^2-2m-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|-\left(m+1\right)^2+2m^2-2m-1\right|}{\sqrt{9+\left(m+1\right)^4}}=1\)
Bạn tự giải ra m nhé

a: y'=3x^2-6
f(1)=1-6+5=0
f'(1)=3-6=-3
y-f(1)=f'(1)(x-1)
=>y-0=-3(x-1)
=>y=-3x+3
b: y=5
=>x^3-6x=0
=>x=0 hoặc x=căn 6 hoặc x=-6
TH1: x=0
y=5; y'=3*0^2-6=-6
Phương trình sẽ là:
y-5=-6(x-0)
=>y=-6x+5
TH2: x=căn 6
y=5; y'=3*6-6=12
Phương trình sẽ là:
y-5=12(x-căn 6)
=>y=12x-12căn 6+5
TH3: x=-căn 6
y=5; y'=12
Phương trình sẽ là:
y-5=12(x+căn 6)
=>y=12x+12căn 6+5

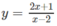

Ta có: y(1) = -3 , y(3) = 7
Từ đó ta có hai phương trình tiếp tuyến phải tìm là:
y + 3 = −5(x – 1) ⇔ y = −5x + 2
y – 7 = −5(x – 3) ⇔ y = −5x + 22