Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: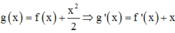 
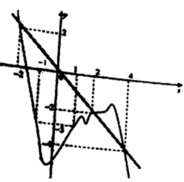
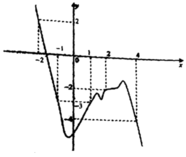
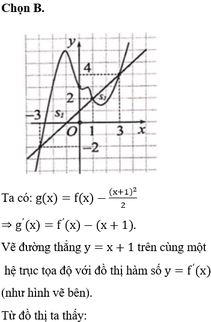
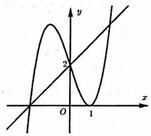
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
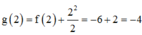
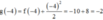
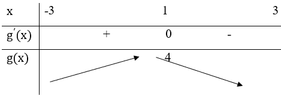
Bảng biến thiên:
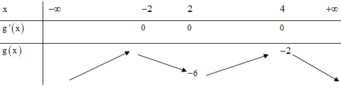
Dựa vào bảng biến thiên ta thấy 
=> phương trình g(x) = 0 không có nghiệm 
Đáp án D
Phương pháp : Nhận xét : f’(x – 2) = f’(x)
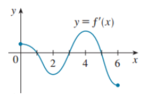
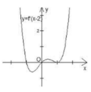
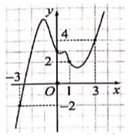
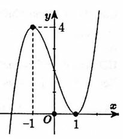
Cách giải : Ta có : f’(x – 2) = (x – 2)’. f’(x) = f’(x) → Đồ thị hàm số y = f’(x) có hình dạng tương tự như trên.
Đồ thị hàm số y = f(x – 2)có 3 điểm cực trị => Đồ thị hàm số y = f(x) cũng có 3 điểm cực trị
Đáp án B
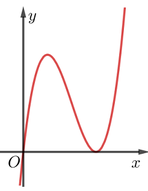
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
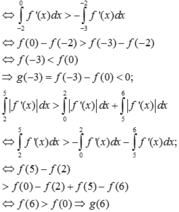
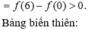
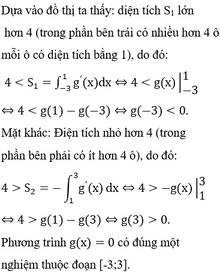
Chọn đáp án C
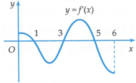
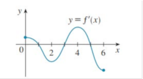
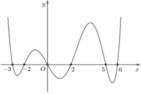
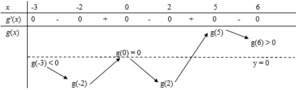
Xét hàm số y = f(x) trên đoạn 0 ; 6 có bảng biến thiên được lập dựa trên đồ thị của hàm số y = f ' x như sau:
Suy ra phương trình f(x) = 0 có tối đa 4 nghiệm.
Đặt g x = f x 2
Xét trên đoạn 0 ; 6 : Phương trình f(x) = 0 có tối đa 4 nghiệm và phương trình f ' x = 0 có 3 nghiệm x ∈ 1 ; 3 ; 5 .
Khi đó phương trình g ' x = 0 có tối đa 7 nghiệm x ∈ 0 ; 6 .
Vậy hàm số y = f x 2 có tối đa 7 điểm cực trị