Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

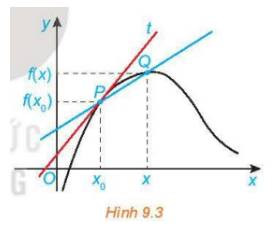
a, Hệ số góc của cát tuyến PQ là \(k_{PQ}=\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}\)
b, Khi \(x\rightarrow x_0\) thì vị trí của điểm \(Q\left(x;f\left(x\right)\right)\) trên đồ thị (C) sẽ tiến gần đến điểm \(P\left(x_0;f\left(x_0\right)\right)\) và khi \(x=x_0\) thì hai điểm này sẽ trùng nhau.
c, Nếu điểm Q di chuyển trên (C) tới điểm P mà \(k_{PQ}\) có giới hạn hữu hạn k thì cát tuyến PQ cũng sẽ tiến đến gần vị trí tiếp tuyến của đồ thị (C) tại điểm P. Vì vậy, giới hạn của cát tuyến QP sẽ là đường thẳng tiếp tuyến tại điểm P

a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
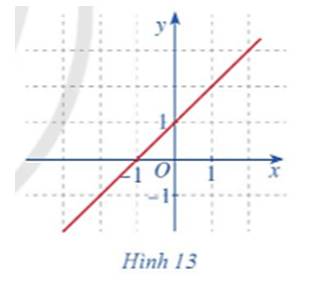
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)

Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = f'\left( {{x_0}} \right);\mathop {\lim }\limits_{x \to {x_0}} \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}} = g'\left( {{x_0}} \right)\)
Vậy \(h'\left( {{x_0}} \right) = f'\left( {{x_0}} \right) + g'\left( {{x_0}} \right)\).

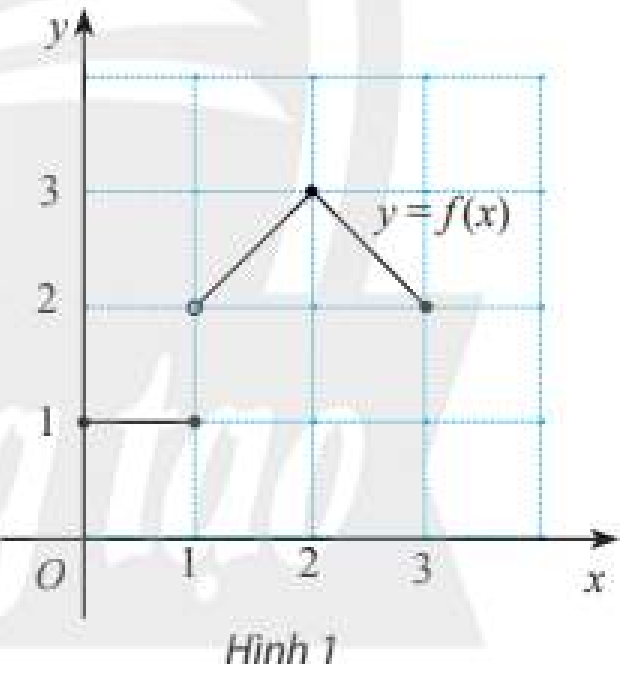
• \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {1 + x} \right) = 1 + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} 1 = 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
• \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {5 - x} \right) = 5 - 2 = 3\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {1 + x} \right) = 1 + 2 = 3\).
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 3\).
Ta có: \(f\left( 2 \right) = 1 + 2 = 3\).
Vậy \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\).

Theo em ý kiến của bạn Nam là đúng.
Ta có: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne g\left( {{x_0}} \right)\)
Do đó \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) + \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne f\left( {{x_0}} \right) + g\left( {{x_0}} \right)\)
Vì vậy hàm số không liên tục tại x0.

a: \(f'\left(x_0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{c-c}{x-x0}=0\)
b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x-x0}{x-x0}=1\)

a) Với mọi điểm \({x_0} \in \left( {1;2} \right)\), ta có: \(f\left( {{x_0}} \right) = {x_0} + 1\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = {x_0} + 1\).
Vì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right) = {x_0} + 1\) nên hàm số \(y = f\left( x \right)\) liên tục tại mỗi điểm \({x_0} \in \left( {1;2} \right)\).
b) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x + 1} \right) = 2 + 1 = 3\).
\(f\left( 2 \right) = 2 + 1 = 3\).
\( \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x + 1} \right) = 1 + 1 = 2\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k \Leftrightarrow 2 = k \Leftrightarrow k = 2\)
Vậy với \(k = 2\) thì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k\).
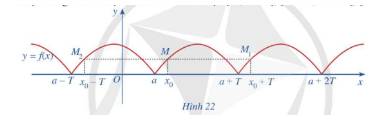

a) Đồ thị hàm số trên mỗi đoạn là như nhau
b) \(f\left( {{x_0} + T} \right) = f\left( {{x_0} - T} \right) = f\left( {{x_0}} \right)\)