Chọn A.

Phương pháp: Sử dụng đạo hàm để tìm giá trị lớn nhất và giá trị nhỏ nhất.

Vậy có 1 số nguyên dương là 3 nằm giữa M và m

Đáp án B.

Từ

f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x

 (1)

Đặt  

f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t

Suy ra   ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và   ∫ 2 x d x = x 2 + C 2

Từ (1) ta suy ra  f 2 x + 1 + C 1 = x 2 + C 2   . Do   f 0 = 0 nên C 2 − C 1 = 1 .

Như vậy  

f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2

⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2

 (do x ∈ 1 ; 3 ).

Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒  Hàm số f x = x x 2 + 2  đồng biến trên R nên f x  cũng đồng biến trên  1 ; 3   .

Khi đó M = max 1 ; 3 f x = f 3 = 3 11  và m = min 1 ; 3 f x = f 1 = 3 .

Vậy 

P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7

Đáp án B

y ' = − 8 x − 3 2 < 0 ;   M = f 0 = 1 3 ;   m = f 2 = − 5. Vậy M + m = 14 3 .

Đáp án B.

ĐK:  0 ≤ x ≤ 1 . Với điều kiện này ta thấy rằng tử là nghịch biên (x tăng thì giá trị tử giảm đi) còn mẫu là đồng biến và mẫu dương (x tăng thì mẫu tăng theo) vì vậy tổng thể hàm y  là hàm nghịch biến. Do đó M = max x ∈ 0 ; 1 y = y 0 = 1 ; m = min x ∈ 0 ; 1 y = y 1 = − 1  vậy  M − m = 2.

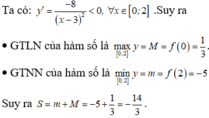
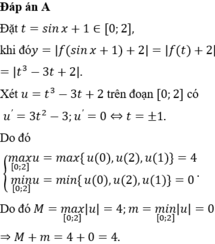
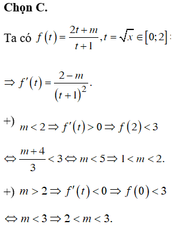
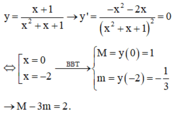
Đáp án C

Đáp án D.