a: Thay x=0 và y=2 vào (d), ta được: 

a=2

b: Thay x=-1 và y=0 vào (d), ta được:

\(-\left(a-2\right)+a=0\)

\(\Leftrightarrow2=0\)(vô lý)

a) Để đồ thị hàm số đi qua điểm A(-2;3), ta thay x = -2 và y = 3 vào phương trình hàm số:
3 = (2m+1)(-2) + 3m - 1
Giải phương trình, ta có:
3 = -4m - 2 + 3m - 1
3 = -m - 3
m = -6

b) Để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2, ta thay x = 2 vào phương trình hàm số:
0 = (2m+1)(2) + 3m - 1
Giải phương trình, ta có:
0 = 4m + 2 + 3m - 1
0 = 7m + 1
m = -1/7

c) Để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, ta thay y = 2 vào phương trình hàm số:
2 = (2m+1)x + 3m - 1
2 = (2m+1)x + 3m - 1
(2m+1)x + 3m = 3

d) Để đồ thị hàm số cắt đường thẳng Y = x + 2 tại điểm có hoành độ bằng 3, ta thay x = 3 vào phương trình hàm số và đường thẳng:
(2m+1)(3) + 3m - 1 = 3 + 2
Giải phương trình, ta có:
6m + 4 = 5
m = 1/6

e) Để đồ thị hàm số cắt đường thẳng Y = -x - 3 tại điểm có tung độ bằng -1, ta thay y = -1 vào phương trình hàm số và đường thẳng:
-1 = (2m+1)x + 3m - 1 = -x - 3
(2m+1)x + 3m = -2

g) Để vẽ đồ thị hàm số khi m = 2, ta thay m = 2 vào phương trình hàm số:
Y = (2(2)+1)x + 3(2) - 1
Y = 5x + 5

a: Thay x=-2 và y=3 vào (d), ta được:

-2(2m+1)+3m-1=3

=>-4m-2+3m-1=3

=>-m-3=3

=>m+3=-3

=>m=-6

b: Thay x=2 và y=0 vào (d), ta được:

2(2m+1)+3m-1=0

=>7m+3=0

=>m=-3/7

c: Thay x=0 và y=2 vào (d), ta được:

0(2m+1)+3m-1=2

=>3m-1=2

=>m=1

d: Thay x=3 vào y=x+2, ta được:

y=3+2=5

Thay x=3; y=5 vào (d), ta được:

3(2m+1)+3m-1=5

=>9m+2=5

=>9m=3

=>m=1/3

e: Thay y=-1 vào y=-x-3, ta được:

-x-3=-1

=>x+3=1

=>x=-2

Thay x=-2 và y=-1 vào (d), ta được:

-2(2m+1)+3m-1=-1

=>-4m-2+3m-1=-1

=>-m-3=-1

=>-m=2

=>m=-2

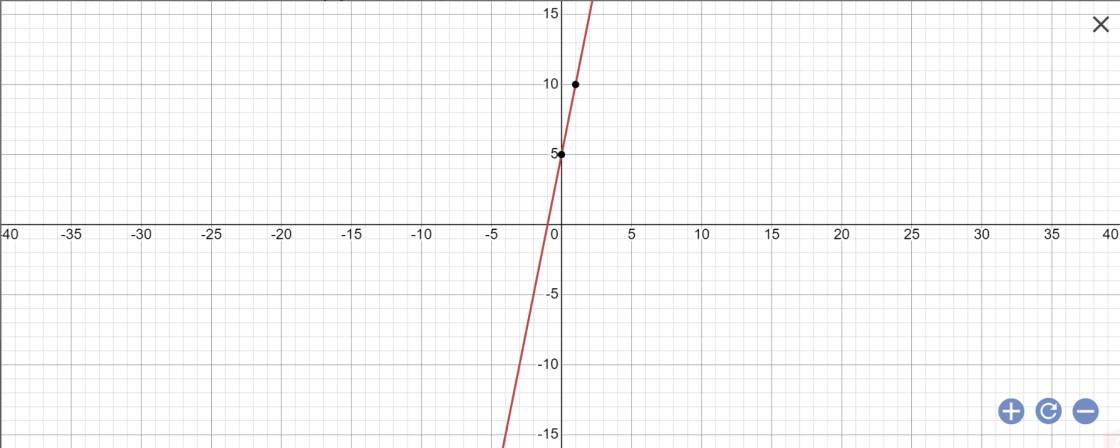
g: Khi m=2 thì (d) sẽ là:

y=(2*2+1)x+3*2-1

=5x+5

......................?

mik ko biết

mong bn thông cảm 

nha ................

Bài 1:

Đặt:  (d):  y = (m+5)x + 2m - 10

Để y là hàm số bậc nhất thì:  m + 5 # 0    <=>   m # -5

Để y là hàm số đồng biến thì: m + 5 > 0  <=>  m > -5

(d) đi qua A(2,3) nên ta có:

3 = (m+5).2 + 2m - 10

<=>  2m + 10 + 2m - 10 = 3

<=>  4m = 3

<=> m = 3/4

(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:

9 = (m+5).0 + 2m - 10

<=> 2m - 10 = 9

<=>  2m = 19

<=> m = 19/2

(d) đi qua điểm 10 trên trục hoành nên ta có:

0 = (m+5).10 + 2m - 10

<=> 10m + 50 + 2m - 10 = 0

<=>  12m = -40

<=> m = -10/3

(d) // y = 2x - 1  nên ta có:

\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\)   <=>   \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\)  <=>  \(m=-3\)

a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2) 

(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2 

<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3 

Vậy (d) : y = -2x - 2 

b, bạn tự vẽ nhé 

c, Cho x = 0 => y = -2 

=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2 

Cho y = 0 => x = -1 

=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1 

Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt ) 

Đặt:  (d):  y = (m+5)x + 2m - 10

Để y là hàm số bậc nhất thì:  m + 5 # 0    <=>   m # -5

Để y là hàm số đồng biến thì: m + 5 > 0  <=>  m > -5

(d) đi qua A(2,3) nên ta có:

3 = (m+5).2 + 2m - 10

<=>  2m + 10 + 2m - 10 = 3

<=>  4m = 3

<=> m = 3/4

(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:

9 = (m+5).0 + 2m - 10

<=> 2m - 10 = 9

<=>  2m = 19

<=> m = 19/2

(d) đi qua điểm 10 trên trục hoành nên ta có:

0 = (m+5).10 + 2m - 10

<=> 10m + 50 + 2m - 10 = 0

<=>  12m = -40

<=> m = -10/3

(d) // y = 2x - 1  nên ta có:

\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1   <=>   \hept{m=−3m≠92\hept{m=−3m≠92  <=>  m=−3

Giả sử (d) luôn đi qua điểm cố định M(x₀; y₀)

Ta có:  y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10

<=>  mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0

<=>  m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0

Để M cố định thì:  \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0   <=>   \hept{x0=−2y0=−20\hept{x0=−2y0=−20

Vậy...

lo n me may

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả. 
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1). 
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2. 
Giao điểm của hai đường tiệm cận là I(1; 2). 
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là 
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)² 
m = 1/(x - 1)² 
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là 
m' = dy/dx = -1/(x - 1)² 
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là 
mm' = -1 
-1/(x - 1)^4 = -1 
(x - 1)^4 = 1 
(x - 1)² = 1 
x - 1 = ±1 
x = 0 hay x = 2 
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)