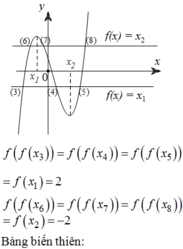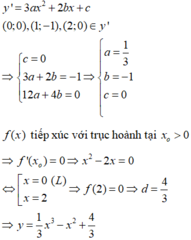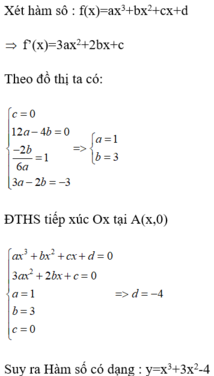Chọn đáp án A.

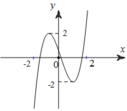
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên  d > 0

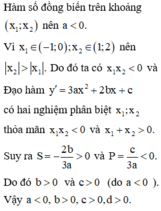
Đáp án A

Đồ thị cắt trục tung tại điểm có tung độ âm ⇒ y 0 = d < 0  

Ta có y ' = 3 a x 2 + 3 b x + c , y ' = 0 ⇔ x 1 + x 2 = - 2 b 3 a x 1 . x 2 = c 3 a . Mà y ' > 0 , ∀ x ∈ x 1 , x 2 ⇒ a < 0  

Mặt khác x 1 + x 2 > 0 x 1 . x 2 < 0 ⇒ - 2 b 3 a > 0 c 3 a < 0 ⇔ b > 0 c < 0 .  Vậy a < 0 , b > 0 , c > 0 , d < 0 .

Đáp án D.

Đáp án D

Ta có:  y ' = 3 a x 2 + 2 b x + c

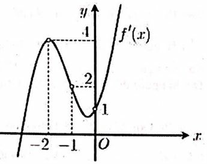
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0

+) Đồ thị hàm số f'(x) có điểm cực trị:

1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1

Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:

f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d

do điểm tiếp xúc có hoành độ dương

=>  d = 4 3 => f(x) cắt trục tung tại điểm có tung độ  4 3

Đáp án D

Chọn C.

Tập xác định: D=R Ta có y = 3 a x 2 + 2 b x + c  

Do đồ thị (C) có hai điểm cực trị nên ta có phương trình y '=0 có hai nghiệm phân biệt hay là phương trình 3 a x 2 + 2 b x + c = 0  có hai nghiệm phân biệt x_i, x_j và hai nghiệm này cũng chính là hoành độ của hai điểm cực trị của đồ thị (C). theo vi-ét ta có x i + x j = - 2 b 3 a .  

Suy ra hoành độ giao điểm nối hai điểm cực trị là

x 0 = x i + x j 2 = 1 3 ⇔ - 2 b 3 a = 2 3 ⇔ b = - a .  

Mặt khác do giả thiết ta có phương trình a x 3 + b x 2 + c x + d = 0  có ba nghiệm phân biệt x₁, x₂, x₃ nên theo vi-ét ta có   x 1 + x 2 + x 3 = - b a = a a = 1 .

Ta có:

3 x 1 + 4 x 2 + 5 x 3 2 = 44 x 1 x 2 + x 2 x 3 + x 3 x 1 ⇔ 9 x 1 2 + 16 x 2 2 + 25 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1  

⇔ 20 3 x 1 2 + 40 3 x 2 2 + x 2 2 + 4 x 3 2 + 7 3 x 1 2 + 21 x 3 2 = 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1  

Áp dụng bất đẳng thức Cauchuy ta có:

• 5 3 4 x 1 2 + 9 x 2 2 ≥ 5 3 . 2 4 x 1 1 . 9 x 2 2 = 20 x 1 x 2  (1).
• x 2 2 + 4 x 3 2 ≥ 2 x 2 2 . 4 x 3 2 = 4 x 1 x 2  (2).
• 7 12 4 x 1 2 + 36 x 3 2 ≥ 7 12 . 2 4 x 1 2 . 36 x 3 2 = 14 x 3 x 1  (3).

Lấy (1) + (2) + (3) vế theo vế ta có: 9 x 1 2 + 16 x 2 2 + 25 x 3 2 ≥ 20 x 1 x 2 + 4 x 2 x 3 + 14 x 3 x 1 .  

Dấu đẳng thức xảy ra khi và chỉ khi:

4 x 1 2 = 9 x 2 2 x 2 2 = 4 x 3 2 4 x 1 2 = 36 x 3 2 x 1 + x 2 + x 3 = 1 ⇔ x 1 = 3 2 x 2 x 2 = 2 x 3 x 3 = 1 3 x 1 x 1 + x 2 + x 3 = 1 ⇔ x 1 = 1 2 x 2 = 1 3 x 3 = 1 6 .  

Vậy S = x 1 + x 2 2 + x 3 2 = 1 2 + 1 3 2 + 1 6 3 = 133 216 .  

Đáp án D