Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với x 0 = 1 thì y 0 = 2016 và f’(1) = 0.
- Do đó, phương trình tiếp tuyến tại điểm có hoành độ x= 1 là
y = 0(x- 1) + 2016 hay y = 2016.

Ta có: y(2) = 21 và y'(2) = 24.
- Do đó, phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = 2 là:
y = 24( x - 2) + 21 hay y = 24x - 27.

Đặt \(y=f(x)=x^3+2x^2+x-1 \)
\(f'(x)=3x^2+4x+1\)
Phương trình tiếp tuyến của đồ thị hàm số y tại M là:
\(y=f'(x_m)(x-x_m)+f(x_m)=f'(1)(x-1)+f(1)=8(x-1)+3=8x-5 \)

Ta có f ' ( x ) = x 2 − x . Gọi x 0 là hoành độ tiếp điểm
f ' ( x 0 ) = 2 ⇔ x 0 2 − x 0 = 2 ⇔ x 0 2 − x 0 − 2 = 0 ⇔ x 0 = 2 x 0 = − 1
* Với x 0 = 2 ⇒ y 0 = 5 3 ⇒ f ' ( 2 ) = 2
Phương trình tiếp tuyến của (C) tại điểm (2 ; 5 3 ) là:
y = 2 ( x − 2 ) + 5 3 = 2 x − 7 3
* Với x 0 = − 1 ⇒ y 0 = 1 6 ⇒ f ' ( − 1 ) = 2
Phương trình tiếp tuyến của (C) tại điểm (-1 ; 1 6 ) là:
y = 2 ( x + 1 ) + 1 6 = 2 x + 13 6
Vậy phương trình tiếp tuyến của (C) tại hệ số góc tiếp tuyến bằng 2 là
y = 2 x − 7 3 ; y = 2 x + 13 6
Chọn đáp án C

a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)

Chọn C
Với x = -1 thì y ( - 1 ) = - ( - 1 ) 3 = 1
Dùng định nghĩa ta tính được y'(-1) = -3. Phương trình tiếp tuyến tại điểm M(-1; 1) là y = -3(x + 1) + 1.

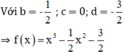
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0
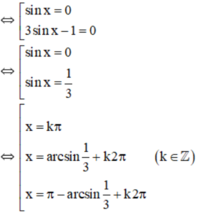
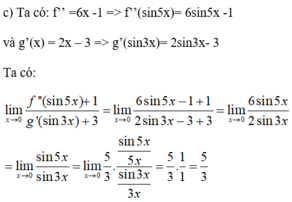
f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11