giúc mk với 

- Vẽ đồ thị hàm số \(y = x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} =  - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

- Vẽ đồ thị hàm số \(y =  - x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y =  - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).

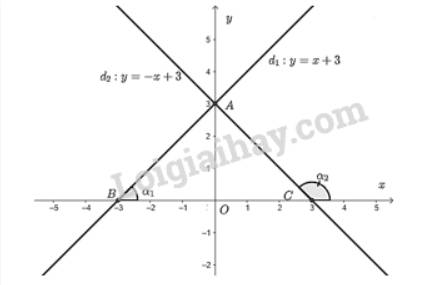
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).

Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).

Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).

a: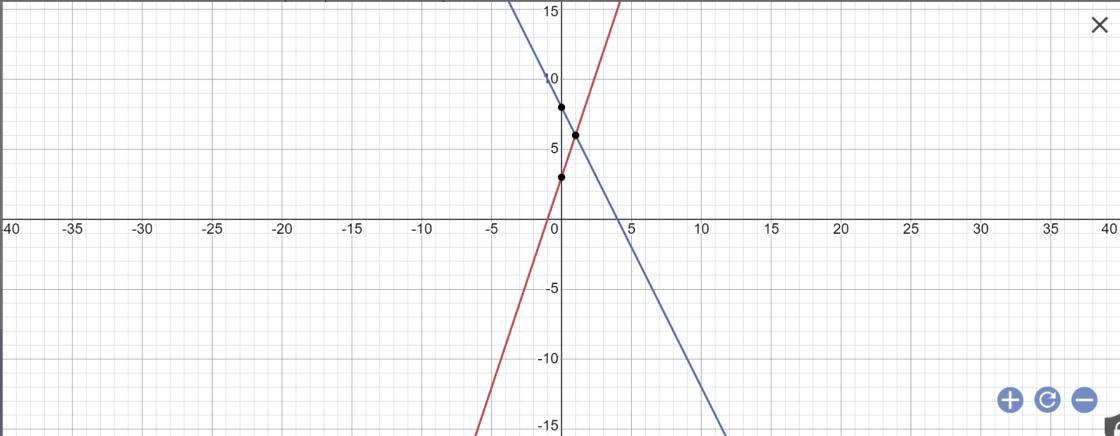 

b: Tọa độ A là:

\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)

Vậy: A(1;6)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)

Vậy: A(1;6); B(-1;0); C(4;0)

\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)

\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)

\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)

=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)

a) * Vẽ đồ thị hàm số \(y =  - \dfrac{1}{2}x + 3\)

Cho x = 0 thì y = 3, ta được điểm P(0; 3) thuộc đồ thị hàm số \(y =  - \dfrac{1}{2}x + 3\)

Cho y = 0 thì x = 6 ta được điểm A(6; 0) thuộc đồ thị hàm số \(y =  - \dfrac{1}{2}x + 3\)

Vậy đồ thị hàm số \(y =  - \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm P(0; 3) và điểm A(6; 0).

* Vẽ đồ thị hàm số y = 2x – 2

Cho x = 0 thì y = -2 ta được điểm Q(0; -2) thuộc đồ thị hàm số y = 2x – 2

Cho y = 0 thì x = 1 ta được điểm B(1; 0) thuộc đồ thị hàm số y = 2x -2

Vậy đồ thị hàm số y = 2x – 2 là đường thẳng đi qua hai điểm Q(0; -2) và B(1; 0)

b) Ta có: A là giao điểm của đường thẳng \(y =  - \dfrac{1}{2}x + 3\) với trục hoành nên \( - \dfrac{1}{2}x + 3 = 0\) suy ra x = 6 nên A(6; 0)

Ta có: B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên 2x – 2 = 0 suy ra x = 1 nên B(1; 0)

Xét phương trình hoành độ giao điểm của hai đường thẳng \(y =  - \dfrac{1}{2}x + 3\) và y = 2x – 2 ta có:

\(\begin{array}{l} - \dfrac{1}{2}x + 3 = 2{\rm{x}} - 2\\ \Rightarrow 3 + 2 = \dfrac{1}{2}x + 2{\rm{x}}\\ \Rightarrow 5 = \dfrac{5}{2}x\\ \Rightarrow x = 2 \Rightarrow y = 2\end{array}\)

Vì C là hoành độ giao điểm của hai đường thẳng \(y =  - \dfrac{1}{2}x + 3\) và y = 2x – 2 nên C(2; 2)

Gọi H là hình chiếu của C lên trục Ox

Khi đó: CH = 2

Mặt khác AB = 5 cm

Diện tích tam giác ABC là; \({S_{ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.2.5 = 5\left( {c{m^2}} \right)\)

a: Tạo độ A là:

\(\left\{{}\begin{matrix}y=0\\-x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-x=-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)

Vậy: O(0;0); A(2;0); B(0;2)

\(OA=\sqrt{\left(2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2}=2\)

\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{2^2}=2\)

b: \(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)

Chu vi tam giác OAB là:

\(C_{OAB}=OA+OB+AB=4+2\sqrt{2}\)

Ta có: Ox\(\perp\)Oy

=>OA\(\perp\)OB

=>ΔOAB vuông tại O

=>\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)

Vì \(Ox \bot Oy\) tại \(O\)nên tam giác \(AOB\) và tam giác \(AOC\) đều vuông tại \(O\).

Ta có: \(OA = 3;OB = 3;OC = 3\)

\(BC = OB + OC = 3 + 3 = 6\).

Áp dụng định lí Py – ta – go cho tam giác \(AOB\) ta có:

\(O{A^2} + O{B^2} = A{B^2}\)

\( \Leftrightarrow {3^2} + {3^2} = A{B^2}\)

\( \Leftrightarrow A{B^2} = 9 + 9 = 18\)

\( \Leftrightarrow AB = \sqrt {18}  = 3\sqrt 2 \)

Áp dụng định lí Py – ta – go cho tam giác \(AOC\) ta có:

\(O{A^2} + O{C^2} = A{C^2}\)

\( \Leftrightarrow {3^2} + {3^2} = A{C^2}\)

\( \Leftrightarrow A{C^2} = 9 + 9 = 18\)

\( \Leftrightarrow AC = \sqrt {18}  = 3\sqrt 2 \)

Chu vi tam giác \(ABC\) là:

\(C = AB + AC + BC = 3\sqrt 2  + 3\sqrt 2  + 6 = 6 + 6\sqrt 2 \) (đơn vị độ dài)

Vì \(Ox \bot Oy\) nên \(OA\) vuông góc với \(BC\) tại \(O\). Do đó, \(OA\) là đường cao  tam giác \(ABC\) ứng với cạnh \(BC\).

Diện tích tam giác \(ABC\) là:

\(S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9\) (đơn vị diện tích)

Vậy chu vi tam giác \(ABC\) là \(6 + 6\sqrt 2 \) đơn vị độ dài và diện tích tam giác \(ABC\) là 9 đơn vị diện tích. 

a)

- Vẽ đồ thị hàm số \(y = x\).

Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).

Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

- Vẽ đồ thị hàm số \(y = x + 2\)

Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).

Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} =  - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).

Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).

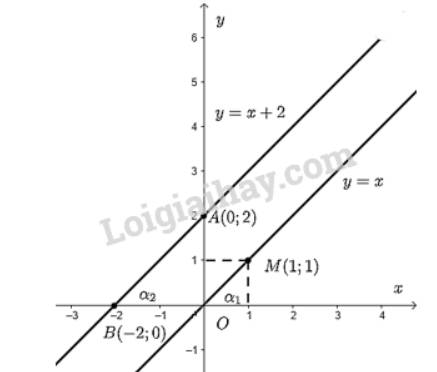
b) Góc tạo bởi hai đường thẳng  \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).

Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).

a: Thay x=1 và y=2 vào (d), ta được:

\(1\left(a-2\right)+b=2\)

=>a-2+b=2

=>a+b=4(1)

Thay x=3và y=-4 vào (d), ta được:

\(3\left(a-2\right)+b=-4\)

=>3a-6+b=-4

=>3a+b=2(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=4\\3a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b-3a-b=2\\a+b=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-2a=2\\a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=4-a=4+2=6\end{matrix}\right.\)

b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:

\(0\left(a-2\right)+b=1-\sqrt{2}\)

=>\(b=1-\sqrt{2}\)

Vậy: (d): \(y=x\left(a-2\right)+1-\sqrt{2}\)

Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:

\(\left(2+\sqrt{2}\right)\left(a-2\right)+1-\sqrt{2}=0\)

=>\(\left(a-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)

=>\(a-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)

=>\(a=\dfrac{3\sqrt{2}}{2}\)

a: Thay x=-1 và y=2 vào (d), ta được:

\(-\left(m-2\right)+n=2\)

=>-m+2+n=2

=>-m+n=0

=>m-n=0(1)

Thay x=3 và y=-4 vào (d), ta được:

\(3\left(m-2\right)+n=-4\)

=>3m-6+n=-4

=>3m+n=2(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}m-n=0\\3m+n=2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m-n+3m+n=2\\m-n=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4m=2\\n=m\end{matrix}\right.\Leftrightarrow n=m=\dfrac{1}{2}\)

b: Thay x=0 và \(y=1-\sqrt{2}\) vào (d), ta được:

\(0\left(m-2\right)+n=1-\sqrt{2}\)

=>\(n=1-\sqrt{2}\)

Vậy: (d): \(y=\left(m-2\right)x+1-\sqrt{2}\)

Thay \(x=2+\sqrt{2}\) và y=0 vào (d), ta được:

\(\left(m-2\right)\cdot\left(2+\sqrt{2}\right)+1-\sqrt{2}=0\)

=>\(\left(m-2\right)\left(2+\sqrt{2}\right)=\sqrt{2}-1\)

=>\(m-2=\dfrac{\sqrt{2}-1}{2+\sqrt{2}}=\dfrac{-4+3\sqrt{2}}{2}\)

=>\(m=\dfrac{-4+3\sqrt{2}+4}{2}=\dfrac{3\sqrt{2}}{2}\)

c: 2y+x-3=0

=>2y=-x+3

=>\(y=-\dfrac{1}{2}x+\dfrac{3}{2}\)

Để (d) vuông góc với đường thẳng y=-1/2x+3/2 thì

\(-\dfrac{1}{2}\left(m-2\right)=-1\)

=>m-2=2

=>m=4

Vậy: (d): \(y=\left(4-2\right)x+n=2x+n\)

Thay x=1 và y=3 vào y=2x+n, ta được:

\(n+2\cdot1=3\)

=>n+2=3

=>n=1

d: 3x+2y=1

=>\(2y=-3x+1\)

=>\(y=-\dfrac{3}{2}x+\dfrac{1}{2}\)

Để (d) song song với đường thẳng \(y=-\dfrac{3}{2}x+\dfrac{1}{2}\) thì

\(\left\{{}\begin{matrix}m-2=-\dfrac{3}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=\dfrac{1}{2}\\n\ne\dfrac{1}{2}\end{matrix}\right.\)

Vậy: (d): \(y=\left(\dfrac{1}{2}-2\right)x+n=-\dfrac{3}{2}x+n\)

Thay x=1 và y=2 vào (d), ta được:

\(n-\dfrac{3}{2}=2\)

=>\(n=2+\dfrac{3}{2}=\dfrac{7}{2}\left(nhận\right)\)