Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(MNPQ\)là hình bình hành.
\(\Rightarrow MQ//NP\)(tính chất).
\(\Rightarrow MQ//PI\).
Xét \(\Delta HMQ\)và \(\Delta HPI\)có:
\(\widehat{MHQ}=\widehat{PHI}\)(vì đối đỉnh).
\(\widehat{QMH}=\widehat{IPH}\)(vì \(MQ//PI\)).
\(\Rightarrow\Delta HMQ~\Delta HPI\left(g.g\right)\)(điều phải chứng minh).

a.) Vì MQ//PI, theo hệ quả định lý ta lét ta có:
\(\dfrac{MQ}{PI}=\dfrac{QH}{IH}=\dfrac{MH}{PH}\)
=> \(\Delta MQH\) ~ \(\Delta PIH\) (c.c.c)
b. Chứng minh tuong tự ta có:
\(\Delta HMK\) ~ \(\Delta HPQ\) (c.c.c)
theo tỉ số \(\dfrac{MK}{PQ}=\dfrac{MK}{MN}=\dfrac{3}{5}\)
Vậy \(\dfrac{S_{HMK}}{S_{HPQ}}=\left(\dfrac{MK}{MN}\right)^2=\left(\dfrac{3}{5}\right)^2=\dfrac{9}{25}\)
c.) Vì MK//PQ => theo ta lét ta có: \(\dfrac{QH}{HK}=\dfrac{HP}{HM}\left(1\right)\)
Vì QM//PI => theo ta lét ta có: \(\dfrac{HP}{HM}=\dfrac{IH}{HQ}\left(2\right)\)
Từ (1) và (2) => \(\dfrac{QH}{HK}=\dfrac{HI}{HQ}=>HQ^2=HI.HK\)

tự vẽ hình nhé
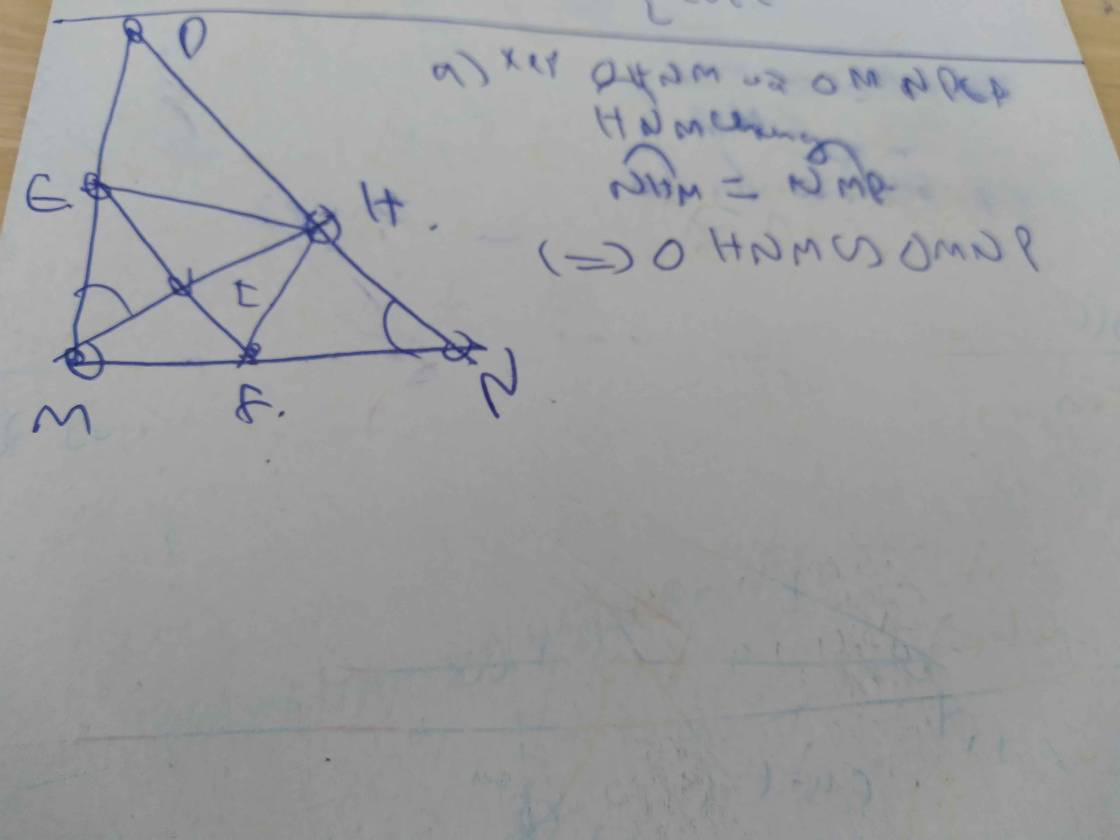
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)

a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP