Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

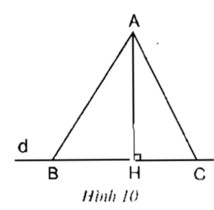
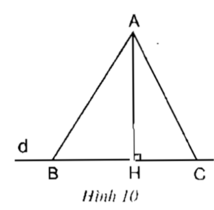
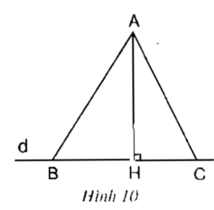
Cho hình AH = 12cm, BH = 5cm, AC = 15cm. Tính AB, HC
. Dùng phương pháp áp dụng định lí Py - ta - go


AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC

Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC

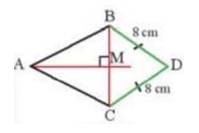
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng

a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)

a: góc B=180-40-70=70 độ
b: Xét ΔDBC có DB=DC
nên ΔDBC cân tại D
=>góc BDC=180 độ-2*góc C=180-2*40=100 độ

- Nếu HB = HC ⇒ HB2 = HC2.
⇒ AH2 + HB2 = AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 = AC2
⇒ AB = AC
- Nếu AB = AC ⇒ AB2 = AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 = AH2 + HC2
⇒ HB2 = HC2
⇒ HB = HC