Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Tính độ dài một cạnh của hình lập phương theo a bằng cách sử dụng định lý Ta-lét

Phương pháp:
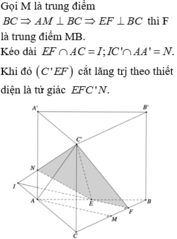
Cắt khối đa diện đã cho làm hai khối: khối lăng trụ và khối tứ diện.
Cách giải:
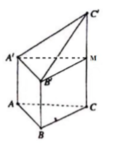
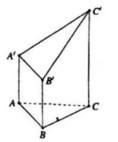
Gọi M là trung điểm của CC’.
Khi đó: khối đa diện đã cho được chia làm 2 phần: Khối lăng trụ tam giác đều A’B’M.ABC và khối tứ diện A’B’C’M.
Thể tích khối lăng trụ tam giác đều A’B’M.ABC là:
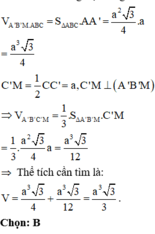

Đáp án D
TXĐ: D = 0 ; 2 ta có: y ' = 2 − 2 x 2 2 x − x 2 < 0 ⇔ x > 1
Do đó hàm số nghịch biến trên 1 ; 2 .

Đáp án D
Khối lập phương có các đỉnh lần lượt là trọng tâm các mặt của khối bát diện đều cạnh a có độ dài cạnh bằng x = 2 3 . a 2 2 = a 2 3 . Vậy thể tích cần tính là V = x 3 = 2 a 3 3 = 8 a 3 27
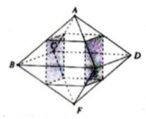

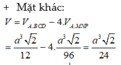
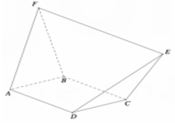
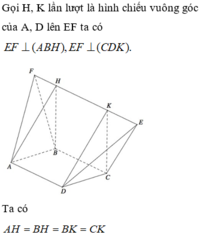
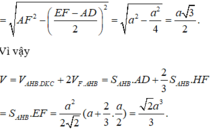
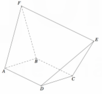
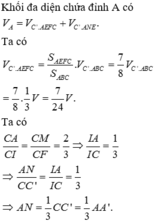
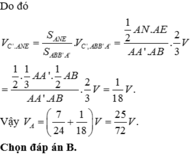
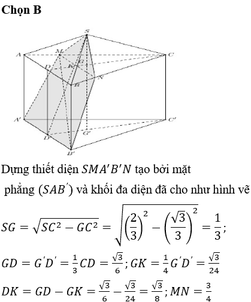
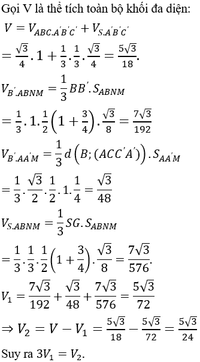
Phương pháp:
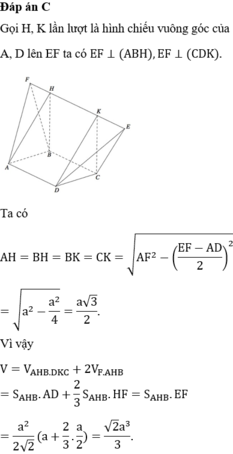
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Cách giải:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh a 2 ;