Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
\(CF=FD=\dfrac{CD}{2}\)(F là trung điểm của CD)
mà AB=CD(Hai cạnh đối của hình bình hành ABCD)
nên AE=CF=FD=EB
Xét tứ giác AECF có
AE//CF(AB//CD, E∈AB, F∈CD)
AE=CF(cmt)
Do đó: AECF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác AEFD có
AE//FD(AB//CD, E∈AB, F∈CD)
AE=FD(cmt)
Do đó: AEFD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
c) Ta có: AF//CE(Hai cạnh đối trong hình bình hành AECF)
mà H∈AF(gt)
và K∈CE(gt)
nên HF//KC và EK//AH
Xét ΔDKC có
F là trung điểm của CD(gt)
FH//DK(cmt)
Do đó: H là trung điểm của DK(Định lí 1 về đường trung bình của tam giác)
⇒DH=KH(1)
Xét ΔABH có
E là trung điểm của AB(gt)
EK//BH(cmt)
Do đó: K là trung điểm của BH(Định lí 1 về đường trung bình của tam giác)
⇒BK=KH(2)
Từ (1) và (2) suy ra DH=HK=KB(đpcm)

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành

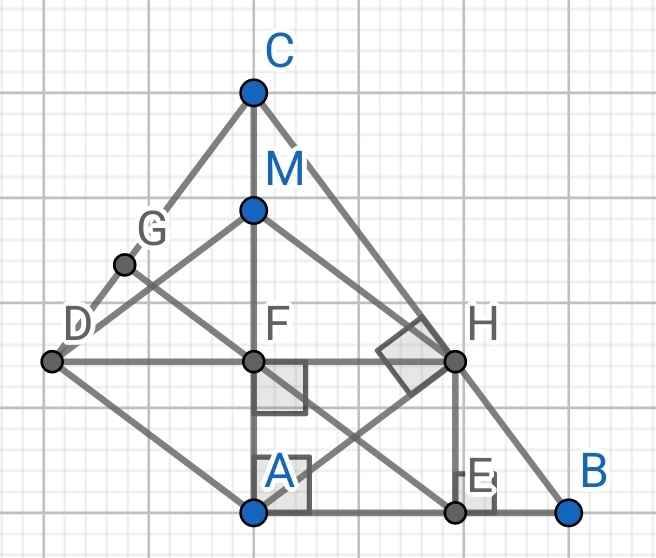 a) Do HE ⊥ AB (gt)
a) Do HE ⊥ AB (gt)
⇒ ∠AEH = 90⁰
Do HF ⊥ AC (gt)
⇒ ∠AFH = 90⁰
Do ∆ABC vuông tại A (gt)
⇒ ∠EAF = 90⁰
Tứ giác AEHF có:
∠AEH = ∠AFH = ∠EAF = 90⁰
⇒ AEHF là hình chữ nhật
b) Do AEHF là hình chữ nhật (cmt)
⇒ HE = AF
Mà AF = FM (do A và M đối xứng qua F)
⇒ HE = FM
Do AEHF là hình chữ nhật (cmt)
⇒ HE // AF
⇒ HE // FM
Tứ giác EFMH có:
HE // FM (cmt)
HE = FM (cmt)
⇒ EFMH là hình bình hành
c) Do A và M đối xứng qua F (gt)
⇒ F là trung điểm của AM
Do D và H đối xứng qua F (gt)
⇒ F là trung điểm của DH
Do HF ⊥ AC (gt)
⇒ HD ⊥ AM
Tứ giác AHMD có:
F là trung điểm của AM (cmt)
F là trung điểm của DH (cmt)
⇒ AHMD là hình bình hành
Mà HD ⊥ AM (cmt)
⇒ AHMD là hình chữ thoi
⇒ AD // MH
Do EFMH là hình bình hành (cmt)
⇒ EF // MH
Mà AD // MH
⇒ EF // AD
Do ADMH là hình thoi (cmt)
⇒ AM là tia phân giác của ∠DAH
⇒ ∠DAM = ∠HAM
⇒ ∠DAC = ∠HAC
Do ADMH là hình thoi
⇒ AD = AH
Xét ∆ADC và ∆AHC có:
AD = AH (cmt)
∠DAC = ∠HAC (cmt)
AC là cạnh chung
⇒ ∆ADC = ∆AHC (c-g-c)
⇒ ∠ADC = ∠AHC = 90⁰ (hai góc tương ứng)
⇒ AD ⊥ DC
Mà EF // AD (cmt)
⇒ EF ⊥ DC
a) Ta chứng minh
b) Tương tự câu a ta chứng minh được
Þ AD.AF =AK.AC (2)
b) Từ (1) ta có AB.AE = AC.AH (3)
Lấy (3) + (2) ta được AD.AF + AB.AE = AC2 (ĐPCM)