Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: BD=căn 8^2+6^2=10cm
BE=10^2/6=100/6=50/3cm
EC=DC^2/BC=8^2/6=32/3cm
Xét ΔEBD có CH//BD
nên CH/BD=EC/EB
=>CH/10=32/50=16/25
=>CH=160/25=6,4cm

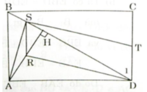
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
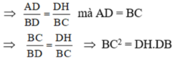
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
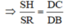
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o

Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB(Hai cạnh đối của hình bình hành ABCD)
\(\widehat{D}=\widehat{B}\)(Hai góc đối của hình bình hành ABCD)
Do đó: ΔAED=ΔCFB(cạnh huyền-góc nhọn)
Suy ra: AE=CF(Hai cạnh tương ứng) và ED=FB(hai cạnh tương ứng)
Ta có: ED+EC=DC(E nằm giữa D và C)
FB+FA=AB(F nằm giữa A và B)
mà AB=DC(Hai cạnh đối của hình bình hành ABCD)
và ED=FB(cmt)
nên EC=FA
Xét tứ giác ECFA có
EC=FA(cmt)
EA=CF(cmt)
Do đó: ECFA là hình bình hành(Dấu hiệu nhận biết hình bình hành)

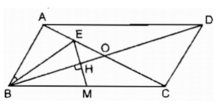
Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 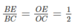
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).